题目内容
(本小题满分12分)如图,在平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上, cm, OC=8cm,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA方向以每秒
cm, OC=8cm,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA方向以每秒 cm的速度匀速运动,Q在线段CO上沿CO方向以每秒1cm的速度匀速运动.设运动时间为t秒.
cm的速度匀速运动,Q在线段CO上沿CO方向以每秒1cm的速度匀速运动.设运动时间为t秒.
(1)用t的式子表示△OPQ的面积S;
(2)求证:四边形OPBQ的面积是一个定值,并求出这个定值;
(3)当△OPQ与△PAB和△QPB相似时,抛物线
 经过B、P两点,过线段BP上一动点M作
经过B、P两点,过线段BP上一动点M作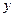 轴的平行线交抛物线于N,当线段MN的长取最大值时,求直线MN把四边形OPBQ分成两部分的面积之比.
轴的平行线交抛物线于N,当线段MN的长取最大值时,求直线MN把四边形OPBQ分成两部分的面积之比.
解:(1) ∵CQ=t,OP= t,CO="8 " ∴OQ=8-t
t,CO="8 " ∴OQ=8-t
∴S△OPQ=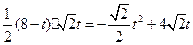 (0<t<8)…………………3分
(0<t<8)…………………3分
(2) ∵S四边形OPBQ=S矩形ABCD-S△PAB-S△CBQ
=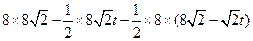 =32
=32 ………… 5分
………… 5分
∴四边形OPBQ的面积为一个定值,且等于32 …………6分
…………6分
(3)当△OPQ与△PAB和△QPB相似时, △QPB必须是一个直角三角形,依题意只能是∠QPB=90°
又∵BQ与AO不平行 ∴∠QPO不可能等于∠PQB,∠APB不可能等于∠PBQ
∴根据相似三角形的对应关系只能是△OPQ∽△PBQ∽△ABP………………8分
∴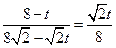 解得:t=4
解得:t=4
经检验:t=4是方程的解且符合题意(从边长关系和速度)
此时P(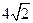 ,0)
,0)
∵B(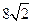 ,8)且抛物线
,8)且抛物线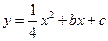 经过B、P两点,
经过B、P两点,
∴抛物线是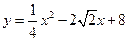 ,直线BP是:
,直线BP是: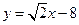 …………………10分
…………………10分
设M(m, )、N(m,
)、N(m,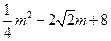 )
)
∵M在BP上运动 ∴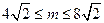
∵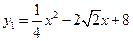 与
与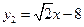 交于P、B两点且抛物线的顶点是P
交于P、B两点且抛物线的顶点是P
∴当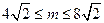 时,
时,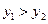 ………………………………11分
………………………………11分
∴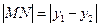 =
=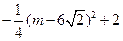 ∴当
∴当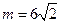 时,MN有最大值是2
时,MN有最大值是2
∴设MN与BQ交于H点则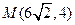 、
、
∴S△BHM=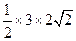 =
=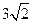
∴S△BHM:S五边形QOPMH=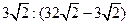 =3:29
=3:29
∴当MN取最大值时两部分面积之比是3:29. …………………12分
解析:
略
 t,CO="8 " ∴OQ=8-t
t,CO="8 " ∴OQ=8-t∴S△OPQ=
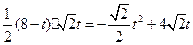 (0<t<8)…………………3分
(0<t<8)…………………3分(2) ∵S四边形OPBQ=S矩形ABCD-S△PAB-S△CBQ
=
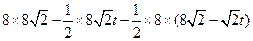 =32
=32 ………… 5分
………… 5分∴四边形OPBQ的面积为一个定值,且等于32
 …………6分
…………6分(3)当△OPQ与△PAB和△QPB相似时, △QPB必须是一个直角三角形,依题意只能是∠QPB=90°
又∵BQ与AO不平行 ∴∠QPO不可能等于∠PQB,∠APB不可能等于∠PBQ
∴根据相似三角形的对应关系只能是△OPQ∽△PBQ∽△ABP………………8分
∴
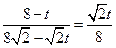 解得:t=4
解得:t=4 经检验:t=4是方程的解且符合题意(从边长关系和速度)
此时P(
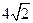 ,0)
,0)∵B(
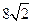 ,8)且抛物线
,8)且抛物线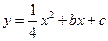 经过B、P两点,
经过B、P两点,∴抛物线是
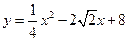 ,直线BP是:
,直线BP是: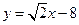 …………………10分
…………………10分设M(m,
 )、N(m,
)、N(m,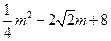 )
) ∵M在BP上运动 ∴
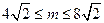
∵
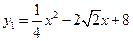 与
与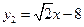 交于P、B两点且抛物线的顶点是P
交于P、B两点且抛物线的顶点是P∴当
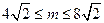 时,
时,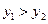 ………………………………11分
………………………………11分∴
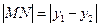 =
=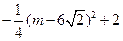 ∴当
∴当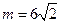 时,MN有最大值是2
时,MN有最大值是2∴设MN与BQ交于H点则
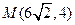 、
、
∴S△BHM=
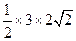 =
=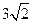
∴S△BHM:S五边形QOPMH=
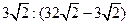 =3:29
=3:29∴当MN取最大值时两部分面积之比是3:29. …………………12分
 |
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的图象经过A、B两点,根据图中信息解答下列问题:
的图象经过A、B两点,根据图中信息解答下列问题:


 同侧,在直线
同侧,在直线 ,连接
,连接 ,与直线
,与直线


