题目内容
已知函数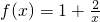 ,其中f(a)表示当x=a时对应的函数值,即
,其中f(a)表示当x=a时对应的函数值,即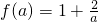 .
.
(1)求f(10);
(2)计算f(1)•f(2)•f(3)…f(100)的值;
(3)如果f(a)-f(a+1)=1,试求a的值.
解:(1)根据题意得:f(10)=1+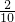 =1
=1 ;
;
(2)∵f(x)=1+ =
= ,
,
∴f(1)•f(2)•f(3)…f(100)
= ×
× ×
× …×
…×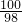 ×
×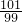 ×
×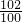
=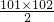
=5151;
(3)∵f(a)=1+ ,f(a+1)=1+
,f(a+1)=1+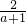 ,且f(a)-f(a+1)=1,
,且f(a)-f(a+1)=1,
∴1+ -(1+
-(1+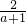 )=1,即
)=1,即 -
-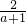 =1,
=1,
去分母得:2(a+1)-2a=a(a+1),即a2+a-2=0,
分解因式得:(a-1)(a+2)=0,
解得:a=1或a=-2,
经检验都符合题意,
则a的值为1或-2.
分析:(1)将x=10代入f(x)解析式中计算,即可得到f(10)的值;
(2)将f(x)解析式通分并利用同分母分式的加法法则化简,列举出f(1),f(2),…,f(100),约分后计算即可得到结果;
(3)表示出f(a)与f(a+1),代入已知的等式中,得到关于a的方程,求出方程的解即可得到a的值.
点评:此题考查了分式的混合运算,分式的加减运算关键是通分,通分的关键是找最简公分母;分式的乘除运算关键是约分,约分的关键是找公因式,约分时分式的分子分母出现多项式,应将多项式分解因式后再约分.
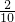 =1
=1 ;
;(2)∵f(x)=1+
 =
= ,
,∴f(1)•f(2)•f(3)…f(100)
=
 ×
× ×
× …×
…×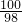 ×
×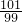 ×
×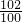
=
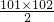
=5151;
(3)∵f(a)=1+
 ,f(a+1)=1+
,f(a+1)=1+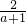 ,且f(a)-f(a+1)=1,
,且f(a)-f(a+1)=1,∴1+
 -(1+
-(1+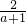 )=1,即
)=1,即 -
-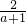 =1,
=1,去分母得:2(a+1)-2a=a(a+1),即a2+a-2=0,
分解因式得:(a-1)(a+2)=0,
解得:a=1或a=-2,
经检验都符合题意,
则a的值为1或-2.
分析:(1)将x=10代入f(x)解析式中计算,即可得到f(10)的值;
(2)将f(x)解析式通分并利用同分母分式的加法法则化简,列举出f(1),f(2),…,f(100),约分后计算即可得到结果;
(3)表示出f(a)与f(a+1),代入已知的等式中,得到关于a的方程,求出方程的解即可得到a的值.
点评:此题考查了分式的混合运算,分式的加减运算关键是通分,通分的关键是找最简公分母;分式的乘除运算关键是约分,约分的关键是找公因式,约分时分式的分子分母出现多项式,应将多项式分解因式后再约分.

练习册系列答案
相关题目
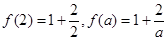 ,则
,则 ,其中
,其中 表示当
表示当 时对应的函数值,如
时对应的函数值,如 ,
, ,则
,则 ……
…… =
=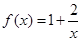 ,其中
,其中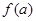 表示当
表示当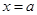 时对应的函数值,即
时对应的函数值,即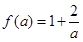 .
.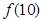 ;
;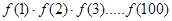 的值;
的值;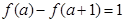 ,试求
,试求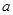 的值.
的值.