题目内容
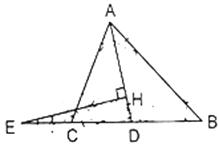
【题目】如图,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,点
,点![]() 在
在![]() 延长线上且
延长线上且![]() 于
于![]() .
.
(1)若![]() ,求
,求![]() 的度数.
的度数.
(2)若![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)105°;(2)20°.
【解析】
(1)根据三角形外角的性质可得∠ADC=75°,再根据垂直的定义可得∠EHD=∠AHE=90°,再根据三角形的内角和定理可求出∠E=15°,再根据三角形外角的性质即可得到![]() 的度数;
的度数;
(2)先根据三角形的内角和定理求出∠BAC的度数,再根据角平分线的性质求出∠CAD=25°,又因为![]() ,有∠AHE=90°,再利用三角形的外角及对顶角相等,可得∠E=∠ACB-(180°-∠AHE-∠CAD),把各角的度数代入即可求出∠E的度数.
,有∠AHE=90°,再利用三角形的外角及对顶角相等,可得∠E=∠ACB-(180°-∠AHE-∠CAD),把各角的度数代入即可求出∠E的度数.
解:∵![]() 是
是![]() 的角平分线,
的角平分线,
∴∠BAD=∠CAD=30°.
∵∠B=45°,
∴∠ADC=75°.
∵![]() ,
,
∴∠EHD=∠AHE=90°,
∴∠E=15°.
∵∠E+∠ACE=∠AHE+∠CAD,
∴∠ACE=90°+30°-15°=105°.
(2)∵∠BAC+∠B+∠ACB=180°, ![]() ,
,![]() ,
,
∴∠BAC=50°,
∵![]() 是
是![]() 的角平分线,
的角平分线,
∴∠CAD=![]() ∠BAC=25°,
∠BAC=25°,
∵∠E+∠ACE=∠CAD+∠AHE,
∴∠E=∠CAD+∠AHE-∠ACE
∵∠ACE=180°-∠ACB=95°,
∴∠E=25°+90°-95°=20°.

【题目】有这样一个问题:探究函数y=-![]() +|x|的图象与性质.
+|x|的图象与性质.
小军根据学习函数的经验,对函数y=-![]() +|x|的图象与性质进行了探究.
+|x|的图象与性质进行了探究.
下面是小军的探究过程,请补充完整:
(1)函数y=-![]() +|x|的自变量x的取值范围是 ;
+|x|的自变量x的取值范围是 ;
(2)表是y与x的几组对应值.
x | -2 | -1.9 | -1.5 | -1 | -0.5 | 0 | 1 | 2 | 3 | 4 | … |
y | 2 | 1.60 | 0.80 | 0 | -0.72 | -1.41 | -0.37 | 0 | 0.76 | 1.55 | … |
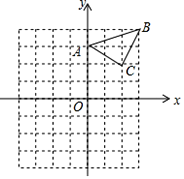
在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;

(3)观察图象,函数的最小值是 ;
(4)进一步探究,结合函数的图象,写出该函数的一条性质(函数最小值除外): .