题目内容
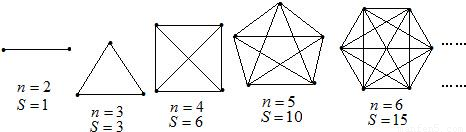
在抗击“非典”的斗争中,某市根据疫情的发展状况,决定全市中、小学放假两周,以切实保障广大中、小学生的安全.腾飞中学初三(1)班的全体同学在自主完成学习任务的同时,不忘关心同学们的安危,两周内全班每两个同学都通过一次电话,互相勉励,共同提高.如果该班有56名同学,那么同学们之间共通了多少次电话为解决该问题,我们可把该班人数n与通电话次数S间的关系用下列模型来表示: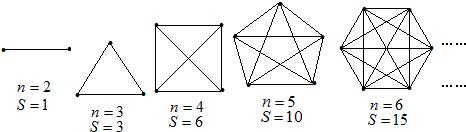
(1)若把n作为点的横坐标,S作为纵坐标,根据上述模型中的数据,在给出的平面直角坐标系中,描出相应各点,并用平滑的曲线连接起来;
(2)根据日中各点的排列规律,猜一猜上述各点会不会在某一函数的图象上如果在,求出该函数的解析式;
(3)根据(2)中得出的函数关系式,求该班56名同学间共通了多少次电话.
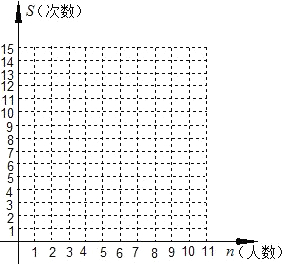
分析:先将各点进行连接,然后观察函数的大致图象,得出是个什么函数,然后设出函数的通式,根据函数经过的点的坐标,用待定系数法求出函数的解析式.然后将n=56代入函数式中即可求出一共通电话的次数.
解答:解:(1)如图:
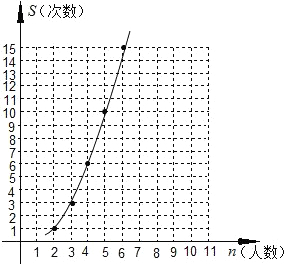
(2)根据图中各点的排列规律,猜想各点可能在一个二次函数的图象上,
设二次函数解析式为:s=an2+bn+c,
∵(2,1)(3,3)(4,6)三点在二次函数图象上,
∴
,
解得:a=
,b=-
,c=0,
∴函数解析式为:s=
n2-
n;
(3)当n=56时,s=
×562-
×56=1540,
即:该班56名同学间共通了1540次电话.

(2)根据图中各点的排列规律,猜想各点可能在一个二次函数的图象上,
设二次函数解析式为:s=an2+bn+c,
∵(2,1)(3,3)(4,6)三点在二次函数图象上,
∴
|
解得:a=
| 1 |
| 2 |
| 1 |
| 2 |
∴函数解析式为:s=
| 1 |
| 2 |
| 1 |
| 2 |
(3)当n=56时,s=
| 1 |
| 2 |
| 1 |
| 2 |
即:该班56名同学间共通了1540次电话.
点评:本题主要考查了二次函数的图形及其应用,画正确图象判定出函数的类型是解题的关键.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目