Question

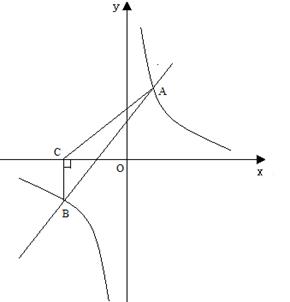
如图，一次函数y＝kx＋b与反比例函数y＝的图象交于A（2，3），B（－3，n）两点．

（1）求一次函数与反比例函数的解析式；

（2）根据所给条件，请直接写出不等式kx＋b＞的解集；

（3）过点B作BC⊥x轴，垂足为C，求S_△ABC．

 

 

 

Answer 1

【答案】

解:（1）∵点A（2，3）在y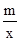＝的图象上，

∴m＝6，

∴反比例函数的解析式为y=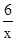

∴n＝＝－2，

∵点A（2，3），B（－3，－2）在y＝kx＋b的图象上，

∴

∴

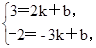
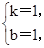
∴一次函数的解析式为y＝x＋1．

（2）－3＜x＜0或x＞2；

（3）设AB交x轴于点D，则D的坐标为（－1,0），

     ∴CD＝2，

     ∴S_△ABC＝S_△BCD＋S_△ACD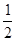＝×2×2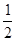＋×2×3＝5．

【解析】（1）要求反比例函数y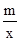＝的解析式，知道它图象上一个点的坐标即可，

要求一次函数y＝kx＋b的解析式，知道图象上两个点的坐标即可。

（2）从图象看即可，交点两个（当x=-3或2时，它们函数值相等），则不等式kx＋b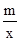＞的解集是两种情况

（3）用分割法，将△ABC分割成两个易求的三角形的面积。