题目内容
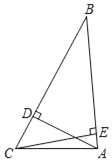
【题目】如图,在Rt△ABC中,∠C=90°,AD=BE=2,点M,P,N分别是DE,BD,AB的中点,则△PMN的周长=___.

【答案】2+![]() .
.
【解析】
先由三角形中位线定理得出PM∥BC,PN∥AC,PM=![]() BE=1,PN=
BE=1,PN=![]() AD=1,再根据平行线的性质得出∠MPD=∠DBC,∠DPN=∠CDB,可证∠MPN=90°,利用勾股定理求出MN=
AD=1,再根据平行线的性质得出∠MPD=∠DBC,∠DPN=∠CDB,可证∠MPN=90°,利用勾股定理求出MN=![]() =
=![]() ,进而得到△PMN的周长.
,进而得到△PMN的周长.
∵点M,P,N分别是DE,BD,AB的中点,AD=BE=2,
∴PM∥BC,PN∥AC,PM=![]() BE=1,PN=
BE=1,PN=![]() AD=1,
AD=1,
∴∠MPD=∠DBC,∠DPN=∠CDB,
∴∠MPD+∠DPN=∠DBC+∠CDB=180°﹣∠C=90°,
即∠MPN=90°,
∴MN=![]() =
=![]() ,
,
∴△PMN的周长=2+![]() .
.
故答案为2+![]() .
.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目