题目内容
【题目】已知函数![]() 的图象经过第四象限的点B(3,a),且与x轴相交于原点和点A(7,0)
的图象经过第四象限的点B(3,a),且与x轴相交于原点和点A(7,0)
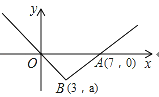
(1)求k、b的值;
(2)当x为何值时,y>﹣2;
(3)点C是坐标轴上的点,如果△ABC恰好是以AB为腰的等腰三角形,直接写出满足条件的点C的坐标
【答案】(1)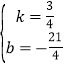 ;(2)x<2或x>
;(2)x<2或x>![]() 时,有y>﹣2;(3)点C的坐标为(2,0)或(12,0)或(-1,0)或(0,1)或(0,-7).
时,有y>﹣2;(3)点C的坐标为(2,0)或(12,0)或(-1,0)或(0,1)或(0,-7).
【解析】
(1)利用待定系数法可得k和b的值;
(2)将y=-2代入函数中,分别计算x的值,根据图象可得结论;
(3)分两种情况画图,以∠BAC和∠ABC为顶角,根据AB=5和对称的性质可得点C的坐标.
(1)当x=3时,a=-3,
∴B(3,-3),
把B(3,-3)和点A(7,0)代入y=kx+b中,
得:![]() ,解得:
,解得: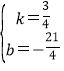 ;
;
(2)当y=-2时,-x=-2,x=2,
![]() ,
,
解得,![]() ,
,
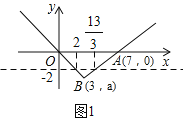
如图1,由图象得:当x<2或x>![]() 时,y>-2;
时,y>-2;
(3)∵B(3,-3)和点A(7,0),
∴AB=![]() =5,
=5,
①以∠BAC为顶角,AB为腰时,如图2,AC=AB=5,
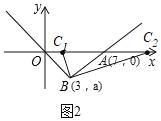
∴C(2,0)或(12,0);
②以∠ABC为顶角,AB为腰时,如图3,以B为圆心,以AB为腰画圆,当△ABC是等腰三角形时,此时存在三个点C,
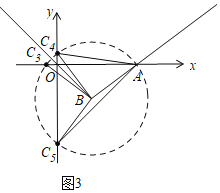
得C3(-1,0),
由C3与C4关于直线 y=-x对称得:C4(0,1)
由C5与点A关于直线y=-x对称得:C5(0,-7)
综上,点C的坐标为(2,0)或(12,0)或(-1,0)或(0,1)或(0,-7).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目