题目内容
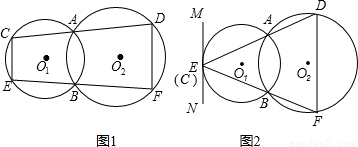
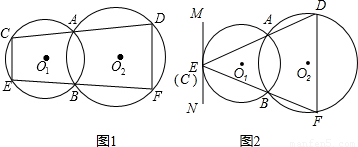
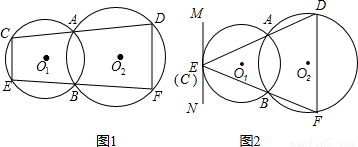
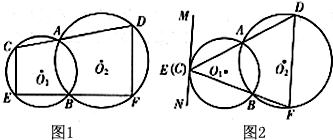
24、如图1,圆O1与圆O2都经过A、B两点,经过点A的直线线CD与圆O1交于点C,与圆O2交于点D.经过点B的直线EF与圆O1交于点E,与圆O2交于点F.
(1)求证:CE∥DF;
(2)在图1中,若CD和EF可以分别绕点A和点B转动,当点C与点E重合时(如图2),过点E作直线MN∥DF,试判断直线MN与圆O1的位置关系,并证明你的结论.

(1)求证:CE∥DF;
(2)在图1中,若CD和EF可以分别绕点A和点B转动,当点C与点E重合时(如图2),过点E作直线MN∥DF,试判断直线MN与圆O1的位置关系,并证明你的结论.
分析:(1)只需连接AB,利用“圆的内接四边形的外角等于内对角”证明∠E+∠F=180°,从而证明CE∥DF;
(2)作辅助线:构造直径所对的圆周角是90°.利用平行线的性质求出∠ABE=∠AHE,根据“圆的内接四边形的外角等于内对角”得出∠D=∠ABE,所以得到∠MEA=∠AHE,∠MEA+∠AEH=90°,利用切线的判定定理,可知MN为圆O1的切线.
(2)作辅助线:构造直径所对的圆周角是90°.利用平行线的性质求出∠ABE=∠AHE,根据“圆的内接四边形的外角等于内对角”得出∠D=∠ABE,所以得到∠MEA=∠AHE,∠MEA+∠AEH=90°,利用切线的判定定理,可知MN为圆O1的切线.
解答: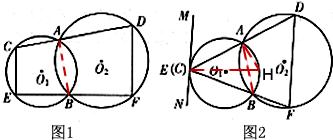 解:(1)连接AB;
解:(1)连接AB;
∵四边形ABEC是圆O1的内接四边形,
∴∠BAD=∠E.
又∵四边形ADFB是圆O2的内接四边形,
∴∠BAD+∠F=180°.
∴∠E+∠F=180°.
∴CE∥DF.
(2)MN与圆O1相切,
过E作圆O1的直径EH,连接AH和AB;
∵MN∥DF,
∴∠MEA=∠D.
又∵∠D=∠ABE,∠ABE=∠AHE,
∴∠MEA=∠AHE.
∵EH为圆O1的直径,
∴∠EAH=90°.
∴∠AHE+∠AEH=90°.
∴∠MEA+∠AEH=90°.
又∵EH为圆O1的直径,
∴MN为圆O1的切线.
 解:(1)连接AB;
解:(1)连接AB;∵四边形ABEC是圆O1的内接四边形,
∴∠BAD=∠E.
又∵四边形ADFB是圆O2的内接四边形,
∴∠BAD+∠F=180°.
∴∠E+∠F=180°.
∴CE∥DF.
(2)MN与圆O1相切,
过E作圆O1的直径EH,连接AH和AB;
∵MN∥DF,
∴∠MEA=∠D.
又∵∠D=∠ABE,∠ABE=∠AHE,
∴∠MEA=∠AHE.
∵EH为圆O1的直径,
∴∠EAH=90°.
∴∠AHE+∠AEH=90°.
∴∠MEA+∠AEH=90°.
又∵EH为圆O1的直径,
∴MN为圆O1的切线.
点评:本题主要考查了相交两圆的性质和圆内接四边形的有关性质.这些基本性质和辅助线的基本作法要掌握.
“圆的内接四边形的外角等于内对角”、“圆的内接四边形的对角互补”是圆内接四边形中的基本性质.
“圆的内接四边形的外角等于内对角”、“圆的内接四边形的对角互补”是圆内接四边形中的基本性质.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目