Question

（2012•响水县一模）动手操作：在矩形纸片ABCD中，AB=3，AD=5，如图所示，折叠纸片，使点A落在BC边上的A₁处，折痕为PQ．当A₁点在BC边上移动时，折痕的端点P、Q也随之移动．若限定点P、Q分别在AB、AD边上移动，则点A₁在BC边上距B点可移动的最短距离为

1

．

Answer 1

分析：由四边形ABCD是矩形，即可得BC=AD=5，CD=AB=3，又由当D与Q重合时，BA₁最小，利用勾股定理，可求得A₁C的值，继而求得BA₁的值．

解答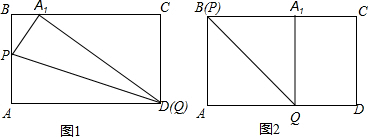：解：∵四边形ABCD是矩形，
∴BC=AD=5，CD=AB=3，
如图1：当D与Q重合时，BA₁最小，
由折叠的性质，可得：A₁D=AD=5，
在Rt△A₁CD中，A₁C=

A1D2-CD2

=4，
∴A₁B=BC-A₁C=5-4=1；
如图2：当B与P重合时，BA₁最大，
此时BA₁=AB=3；
∴点A₁在BC边上距B点可移动的最短距离为1．
故答案为：1．

点评：此题考查了折叠的性质、矩形的性质以及勾股定理．此题难度适中，注意掌握数形结合思想的应用．