题目内容
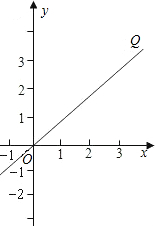 如图,直线OQ的函数解析式为y=x.
如图,直线OQ的函数解析式为y=x.下表是直线a的函数关系中自变量x与函数y的部分对应值.
| x | … | -1 | 1 | 2 | 3 | … |
| y | … | 8 | 4 | 2 | 0 | … |
(1)根据表所提供的信息,请在直线OQ所在的平面直角坐标系中画出直线a的图象,并说明点(10,-10)不在直线a的图象上;
(2)求点C的坐标;
(3)设△OBC中位于直线l左侧部分的面积为S,写出S与m之间的函数关系式;
(4)试问是否存在点P,使过点P且垂直于x轴的直线l平分△OBC的面积?若有,求出点P坐标;若无,请说明理由.
分析:(1)利用表中信息,描点、连线即可得到a的图象,由图象可知这是一个一次函数的图象,所以选择其中的两个点,
由待定系数法可求得直线a的解析式为y=-2x+6,然后判断点(10,-10)的坐标是否满足y=-2x+6,从而做出判断;
(2)因为直线a与直线OQ交点为C,所以将两函数的解析式联立,得到方程组,解方程组即可求出交点的坐标;
(3)由(2)知,P(2,2),因为动点P(m,0)(0<m<3)在OB上移动,过点P作直线l与x轴垂直,所以需要分情况讨论:
当0<m≤2时,P在直线OQ上,所以△OBC中位于直线l左侧部分是一个等腰直角三角形,S=
m2;
当2<m<3时,P在直线BC上,所以△OBC中位于直线l右侧部分是一个直角三角形S=
×3×2-
(3-m)•(-2m+6);
(4)若有这样的P点,使直线l平分△OBC的面积,很显然0<m<2,由于△OBC面积等于3,故当l平分△OBC面积时,S=
,所以
m2=
,解之即可.
由待定系数法可求得直线a的解析式为y=-2x+6,然后判断点(10,-10)的坐标是否满足y=-2x+6,从而做出判断;
(2)因为直线a与直线OQ交点为C,所以将两函数的解析式联立,得到方程组,解方程组即可求出交点的坐标;
(3)由(2)知,P(2,2),因为动点P(m,0)(0<m<3)在OB上移动,过点P作直线l与x轴垂直,所以需要分情况讨论:
当0<m≤2时,P在直线OQ上,所以△OBC中位于直线l左侧部分是一个等腰直角三角形,S=
| 1 |
| 2 |
当2<m<3时,P在直线BC上,所以△OBC中位于直线l右侧部分是一个直角三角形S=
| 1 |
| 2 |
| 1 |
| 2 |
(4)若有这样的P点,使直线l平分△OBC的面积,很显然0<m<2,由于△OBC面积等于3,故当l平分△OBC面积时,S=
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
解答:解:(1)由表中信息可知点(2,2),(3,0)在直线a上,描点连线得直线a的图象,如图.(1分)
由待定系数法可求得直线a的解析式为y=-2x+6(3分)
点(10,-10)的坐标不满足y=-2x+6
所以点(10,-10)不在直线a图象上(4分)
(2)解方程组
(6分)
得x=y=2
故点C的坐标为(2,2)(8分)
(3)当0<m≤2时,如图(1),∵C的坐标是(2,2),作CD⊥x轴,则△OCD是等腰直角三角形,则△OPM也是等腰直角三角形.
则OP=PM=x,则
S=
m2(11分)
当2<m<3时,如图(2),NP=3-m,
∵△NCD∽△NMP,
∴
=
,
则MP=-2m+6,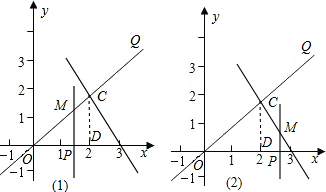
S=S△ONC-S△NPM
=
×3×2-
(3-m)•(-2m+6)(13分)
=-m2+6m-6(14分)
(4)若有这样的P点,使直线l平分△OBC的面积,很显然0<m<2(16分)
由于△OBC面积等于3,故当l平分△OBC面积时,S=
∴
m2=
解得m=
故存在这样的P点,使l平分△OBC的面积.
点P的坐标为(
,0).(20分)
由待定系数法可求得直线a的解析式为y=-2x+6(3分)
点(10,-10)的坐标不满足y=-2x+6
所以点(10,-10)不在直线a图象上(4分)
(2)解方程组
|
得x=y=2
故点C的坐标为(2,2)(8分)
(3)当0<m≤2时,如图(1),∵C的坐标是(2,2),作CD⊥x轴,则△OCD是等腰直角三角形,则△OPM也是等腰直角三角形.
则OP=PM=x,则
S=
| 1 |
| 2 |
当2<m<3时,如图(2),NP=3-m,
∵△NCD∽△NMP,
∴
| MP |
| CD |
| NP |
| ND |
则MP=-2m+6,

S=S△ONC-S△NPM
=
| 1 |
| 2 |
| 1 |
| 2 |
=-m2+6m-6(14分)
(4)若有这样的P点,使直线l平分△OBC的面积,很显然0<m<2(16分)
由于△OBC面积等于3,故当l平分△OBC面积时,S=
| 3 |
| 2 |
∴
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
故存在这样的P点,使l平分△OBC的面积.
点P的坐标为(
| 3 |
点评:解决本题这类问题常用到分类讨论、数形结合、方程和转化等数学思想方法.

练习册系列答案
相关题目
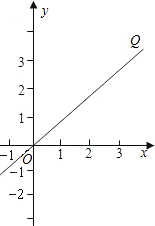 如图,直线OQ的函数解析式为y=x.
如图,直线OQ的函数解析式为y=x.
下表是直线a的函数关系中自变量x与函数y的部分对应值.
| x | … | -1 | 1 | 2 | 3 | … |
| y | … | 8 | 4 | 2 | 0 | … |
设直线a与x轴交点为B,与直线OQ交点为C,动点P(m,0)(0<m<3)在OB上移动,过点P作直线l与x轴垂直.
(1)根据表所提供的信息,请在直线OQ所在的平面直角坐标系中画出直线a的图象,并说明点(10,-10)不在直线a的图象上;
(2)求点C的坐标;
(3)设△OBC中位于直线l左侧部分的面积为S,写出S与m之间的函数关系式;
(4)试问是否存在点P,使过点P且垂直于x轴的直线l平分△OBC的面积?若有,求出点P坐标;若无,请说明理由.
| 如图,直线OQ的函数解析式为y=x,下表是直线a的函数关系中自变量x与函数y的部分对应值: | ||||||||||||||
| ||||||||||||||
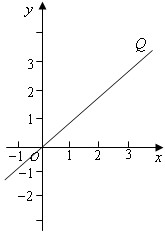 | ||||||||||||||
| (1)根据表所提供的信息,请在直线OQ所在的平面直角坐标系中画出直线a的图象,并说明点(10,-10)不在直线a的图象上; (2)求点C的坐标; (3)设△OBC中位于直线l左侧部分的面积为S,写出S与m之间的函数关系式; (4)试问是否存在点P,使过点P且垂直于x轴的直线l平分△OBC的面积?若有,求出点P坐标;若无,请说明理由。 |
(2006•湘西州)如图,直线OQ的函数解析式为y=x.
下表是直线a的函数关系中自变量x与函数y的部分对应值.
设直线a与x轴交点为B,与直线OQ交点为C,动点P(m,0)(0<m<3)在OB上移动,过点P作直线l与x轴垂直.
(1)根据表所提供的信息,请在直线OQ所在的平面直角坐标系中画出直线a的图象,并说明点(10,-10)不在直线a的图象上;
(2)求点C的坐标;
(3)设△OBC中位于直线l左侧部分的面积为S,写出S与m之间的函数关系式;
(4)试问是否存在点P,使过点P且垂直于x轴的直线l平分△OBC的面积?若有,求出点P坐标;若无,请说明理由.

下表是直线a的函数关系中自变量x与函数y的部分对应值.
| x | … | -1 | 1 | 2 | 3 | … |
| y | … | 8 | 4 | 2 | 0 | … |
(1)根据表所提供的信息,请在直线OQ所在的平面直角坐标系中画出直线a的图象,并说明点(10,-10)不在直线a的图象上;
(2)求点C的坐标;
(3)设△OBC中位于直线l左侧部分的面积为S,写出S与m之间的函数关系式;
(4)试问是否存在点P,使过点P且垂直于x轴的直线l平分△OBC的面积?若有,求出点P坐标;若无,请说明理由.

(2006•湘西州)如图,直线OQ的函数解析式为y=x.
下表是直线a的函数关系中自变量x与函数y的部分对应值.
设直线a与x轴交点为B,与直线OQ交点为C,动点P(m,0)(0<m<3)在OB上移动,过点P作直线l与x轴垂直.
(1)根据表所提供的信息,请在直线OQ所在的平面直角坐标系中画出直线a的图象,并说明点(10,-10)不在直线a的图象上;
(2)求点C的坐标;
(3)设△OBC中位于直线l左侧部分的面积为S,写出S与m之间的函数关系式;
(4)试问是否存在点P,使过点P且垂直于x轴的直线l平分△OBC的面积?若有,求出点P坐标;若无,请说明理由.

下表是直线a的函数关系中自变量x与函数y的部分对应值.
| x | … | -1 | 1 | 2 | 3 | … |
| y | … | 8 | 4 | 2 | 0 | … |
(1)根据表所提供的信息,请在直线OQ所在的平面直角坐标系中画出直线a的图象,并说明点(10,-10)不在直线a的图象上;
(2)求点C的坐标;
(3)设△OBC中位于直线l左侧部分的面积为S,写出S与m之间的函数关系式;
(4)试问是否存在点P,使过点P且垂直于x轴的直线l平分△OBC的面积?若有,求出点P坐标;若无,请说明理由.
