题目内容
【题目】如图,在△ABC中,∠ACB=90°,BC=15,AC=20,CD是高.
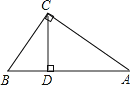
(1)求AB的长;
(2)求△ABC的面积;
(3)求CD的长.
【答案】(1)AB的长是25;(2)△ABC的面积是150;(3) CD的长是12.
【解析】
试题分析:(1)根据勾股定理可求得AB的长;
(2)根据三角形的面积公式计算即可求解;
(3)根据三角形的面积相等即可求得CD的长.
试题解析:(1)∵在△ABC中,∠ACB=90°,BC=15,AC=20,
∴AB2=AC2+BC2,
解得AB=25.
答:AB的长是25;
(2)![]() ACBC=
ACBC=![]() ×20×15=150.
×20×15=150.
答:△ABC的面积是150;
(3)∵CD是边AB上的高,
∴![]() ACBC=
ACBC=![]() ABCD,
ABCD,
解得:CD=12.
答:CD的长是12.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目