��Ŀ����
 ��2009•������ģ����ͼ��ʾ��Rt��ABC�У���C=90�㣬AC=6��BC=12����P�ӵ�A������AC�����C��ÿ��1����λ���ٶ��ƶ�����Q�ӵ�C������CB�����B��ÿ��1����λ���ٶ��ƶ�����P��Qͬʱ���������ƶ�ʱ��Ϊt�루t��0����
��2009•������ģ����ͼ��ʾ��Rt��ABC�У���C=90�㣬AC=6��BC=12����P�ӵ�A������AC�����C��ÿ��1����λ���ٶ��ƶ�����Q�ӵ�C������CB�����B��ÿ��1����λ���ٶ��ƶ�����P��Qͬʱ���������ƶ�ʱ��Ϊt�루t��0������1����tΪ��ֵʱ��PQ��AB��
��2�����PCQ�����Ϊy����y��t�ĺ�����ϵʽ���������tΪ��ֵʱ����PCQ���������������Ƕ��٣�
��3�����C����ֱ��PQ�ĶԳƵ�ΪD����tΪ��ֵʱ���ı���PCQD�������Σ�
��4�����õ�������PCQD��P������AC���ƶ�����������PCQD��CB����B����ÿ��1����λ���ٶ��ƶ�������Q���B�غ�ʱ��ֹͣ�ƶ������˶��е�������ΪMNQD��������MNQD��Rt��ABC�غϲ��ֵ����ΪS����S��t�ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
��������1������PQ��AB���ó�
=
���������t��ֵ���ɣ�
��2������y=
PC��CQ�ó�����t�Ķ��κ����Ľ���ʽ�����������ֵ���ɣ�
��3�����õ�PC=CQʱ��t=3����PCQ�ǵ���ֱ�������Σ������ó���t=3ʱ������PCQ���۵õ����ı���PCQD�������Σ�
��4�����ݵ�t=6ʱ����6��t��9ʱ����D��Rt��ABC���ⲿ����M��Rt��ABC���ڲ����Լ���9��t��12����D��M����Rt��ABC���ⲿ�ֱ�������ɣ�
| PC |
| AC |
| CQ |
| CB |
��2������y=
| 1 |
| 2 |
��3�����õ�PC=CQʱ��t=3����PCQ�ǵ���ֱ�������Σ������ó���t=3ʱ������PCQ���۵õ����ı���PCQD�������Σ�
��4�����ݵ�t=6ʱ����6��t��9ʱ����D��Rt��ABC���ⲿ����M��Rt��ABC���ڲ����Լ���9��t��12����D��M����Rt��ABC���ⲿ�ֱ�������ɣ�
���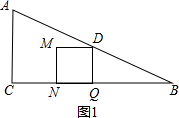 �⣺��1��������ó���CQ=t��PC=6-t��
�⣺��1��������ó���CQ=t��PC=6-t��
��PQ��AB��
��
=
��
��
=
��
��t=4��
��2����y=
PC��CQ=-
t2+3t=-
��t-3��2+
��
��t=3ʱ����PCQ��������������Ϊ��
��
��3���ߵ�PC=CQʱ��t=3����PCQ�ǵ���ֱ�������Σ�
�൱t=3ʱ������PCQ���۵õ����ı���PCQD�������Σ�
��4������ͼ1������֪������֪����t=6ʱ��������MNQD�Ķ���D����б��AB���е㣬
�൱3��t��6ʱ��������MNQD��Rt��ABC���ڲ�����ʱs=9��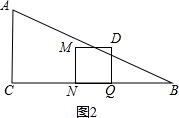
����ͼ2����6��t��9ʱ����D��Rt��ABC���ⲿ����M��Rt��ABC���ڲ�����������MNQD��
AB����������ֱ���E��F����BQ=12-t��
�������DQ��AC��
��
=
��
��
=
��
��EQ=6-
t��
DE=3-EQ=
t-3��
���������DF=t-6��
��S=9-
DE��DF=-
t2+3t��
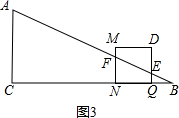
����ͼ3����9��t��12��
��D��M����Rt��ABC���ⲿ����������MNQD��AB����������Ϊ��E��F��
�������
BQ=12-t��
��QE=
��12-t����
��BN=BQ+NQ=15-t��
��FN=
��15-t����
��S=
��QE+FN����3=-
t+
��
 �⣺��1��������ó���CQ=t��PC=6-t��
�⣺��1��������ó���CQ=t��PC=6-t����PQ��AB��
��
| PC |
| AC |
| CQ |
| CB |
��
| 6-t |
| 6 |
| t |
| 12 |
��t=4��
��2����y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
��t=3ʱ����PCQ��������������Ϊ��
| 9 |
| 2 |
��3���ߵ�PC=CQʱ��t=3����PCQ�ǵ���ֱ�������Σ�
�൱t=3ʱ������PCQ���۵õ����ı���PCQD�������Σ�
��4������ͼ1������֪������֪����t=6ʱ��������MNQD�Ķ���D����б��AB���е㣬
�൱3��t��6ʱ��������MNQD��Rt��ABC���ڲ�����ʱs=9��

����ͼ2����6��t��9ʱ����D��Rt��ABC���ⲿ����M��Rt��ABC���ڲ�����������MNQD��
AB����������ֱ���E��F����BQ=12-t��
�������DQ��AC��
��
| EQ |
| AC |
| QB |
| BC |
��
| EQ |
| BQ |
| 1 |
| 2 |
��EQ=6-
| 1 |
| 2 |
DE=3-EQ=
| 1 |
| 2 |
���������DF=t-6��
��S=9-
| 1 |
| 2 |
| 1 |
| 4 |
����ͼ3����9��t��12��
��D��M����Rt��ABC���ⲿ����������MNQD��AB����������Ϊ��E��F��
�������

BQ=12-t��
��QE=
| 1 |
| 2 |
��BN=BQ+NQ=15-t��
��FN=
| 1 |
| 2 |
��S=
| 1 |
| 2 |
| 3 |
| 2 |
| 81 |
| 4 |
������������Ҫ�����˷��۱任�������Լ������ε����ʣ����÷�������˼����з������ɵó����ǽ���ؼ���

��ϰ��ϵ�д�
�����Ŀ
 ��2009•������ģ����ͼ��AB�ǡ�O��ֱ����C��AB�ӳ�����һ�㣬BC=OB��CD�С�O��D�����A�Ķ�����
��2009•������ģ����ͼ��AB�ǡ�O��ֱ����C��AB�ӳ�����һ�㣬BC=OB��CD�С�O��D�����A�Ķ�����