题目内容
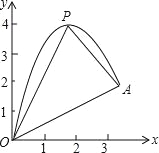
【题目】如图，一小球从斜坡O点处抛出，球的抛出路线可以用二次函数y=﹣x2+4x刻画，斜坡可以用一次函数y=
x刻画．
（1）请用配方法求二次函数图象的最高点P的坐标；
（2）小球的落点是A，求点A的坐标；
（3）连接抛物线的最高点P与点O、A得△POA，求△POA的面积；
（4）在OA上方的抛物线上存在一点M（M与P不重合），△MOA的面积等于△POA的面积．请直接写出点M的坐标．
【答案】（1）最高点P的坐标为（2，4）；（2）点A的坐标为（
，
）；（3）
；（4）点M的坐标为（
，
）．
【解析】
试题分析：（1）利用配方法抛物线的一般式化为顶点式，即可求出二次函数图象的最高点P的坐标；
（2）联立两解析式，可求出交点A的坐标；
（3）作PQ⊥x轴于点Q，AB⊥x轴于点B．根据S△POA=S△POQ+S△梯形PQBA﹣S△BOA，代入数值计算即可求解；
（4）过P作OA的平行线，交抛物线于点M，连结OM、AM，由于两平行线之间的距离相等，根据同底等高的两个三角形面积相等，可得△MOA的面积等于△POA的面积．设直线PM的解析式为y=
x+b，将P（2，4）代入，求出直线PM的解析式为y=x+3．再与抛物线的解析式联立，得到方程组
，解方程组即可求出点M的坐标．
试题解析：（1）由题意得，y=﹣x2+4x=﹣（x﹣2）2+4，
故二次函数图象的最高点P的坐标为（2，4）；
（2）联立两解析式可得：
，解得：
，或
．
故可得点A的坐标为（，）；
（3）如图，作PQ⊥x轴于点Q，AB⊥x轴于点B．
S△POA=S△POQ+S△梯形PQBA﹣S△BOA
=×2×4+×（+4）×（﹣2）﹣××
=4+
﹣
=；
（4）过P作OA的平行线，交抛物线于点M，连结OM、AM，则△MOA的面积等于△POA的面积．
设直线PM的解析式为y=x+b，
∵P的坐标为（2，4），
∴4=×2+b，解得b=3，
∴直线PM的解析式为y=x+3．
由，解得
，
，
∴点M的坐标为（，）．
