Question

我们给出如下定义：有一组相邻内角相等的四边形叫做等邻角四边形．请解答下列问题：
（1）写出一个你所学过的特殊四边形中是等邻角四边形的图形的名称；
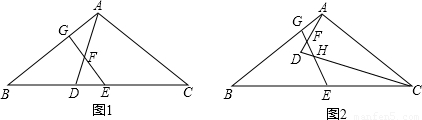
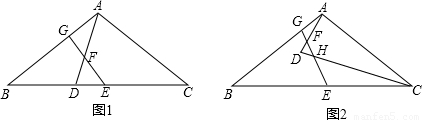
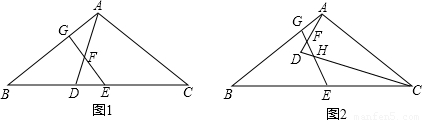
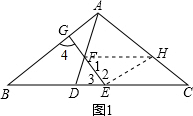
（2）如图1，在△ABC中，AB=AC，点D在BC上，且CD=CA，点E、F分别为BC、AD的中点，连接EF并延长交AB于点G．求证：四边形AGEC是等邻角四边形；
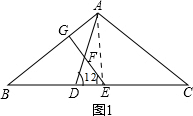
（3）如图2，若点D在△ABC的内部，（2）中的其他条件不变，EF与CD交于点H，图中是否存在等邻角四边形，若存在，指出是哪个四边形，不必证明；若不存在，请说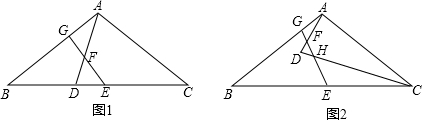明理由．

Answer 1

解：（1）等腰梯形（或矩形，或正方形）

（2）证法一：取AC的中点H，连接HE、HF
∵点E为BC中点
∴EH为△ABC的中位线
∴EH∥AB，且EH=AB
同理FH∥DC，且FH=DC
∵AB=AC，DC=AC
∴AB=DC，EH=FH
∴∠1=∠2
∵EH∥AB，FH∥DC
∴∠2=∠4，∠1=∠3
∴∠4=∠3
∵∠AGE+∠4=180°，∠GEC+∠3=180°
∴∠AGE=∠GEC
∴四边形AGEC是邻角四边形
证法二：连接AE
设∠B的度数为x
∵AB=AC，CD=CA
∴∠C=∠B=x，∠1=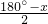=90°-
∵F是AD的中点
∴AF=DF=AD
∴∠2=∠1=90°-
∴∠AGE=∠B+∠2=x+90°-=90°+
∠GEC=180°-（90°-）=90°+
∴∠AGE=∠GEC
∴四边形AGEC是邻角四边形

（3）存在等邻角四边形，为四边形AGHC．
分析：（1）邻角相等的四边形有很多，矩形、正方形或者等腰梯形都至少有一组邻角相等．
（2）解本题有两种方法：①运用中位线的性质，找出对应相等的角；②用待定系数法，设出x，写出关于x的代数式，化简即可找出对应相等的角．
（3）根据题意易知满足条件的四边形即为第二题的四边形．
点评：本题考查了三角形的角的性质以及等腰三角形的性质的综合运用．本题较灵活，要求学生能够把题中的条件转化成角，从而找出相等的角来解题．