Question

设Rt△ABC中，∠C=90°，∠A、∠B、∠C的对边分别为a、b、c，根据下列所给条件求∠B的四个三角函数值：（自己画图）
（1）a=1，c=2；（2）a=5，b=12．

Answer 1

分析：利用勾股定理可得第三边的长．sinB=

b

c

，cosB=

a

c

，tanB=

b

a

，cotB=

a

b

，把相关数值代入即可．

解答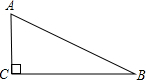：解：（1）∵a=1，c=2，
∴b=

c2-a2

=

3

，
∴sinB=

b

c

=

3

2

，
cosB=

a

c

=

1

2

，
tanB=

b

a

=

3

，
cotB=

a

b

=

1

3

=

3

3

；

（2）∵a=5，b=12．
∴c=

a2+b2

=13，
sinB=

b

c

=

12

13

，
cosB=

a

c

=

5

13

，
tanB=

b

a

=

12

5

，
cotB=

a

b

=

5

12

．

点评：考查锐角三角函数的应用；利用勾股定理得到第三边是解决本题的突破点；熟记相应∠B的三角函数是解决本题的关键．