题目内容
a,b,c都是两位整数,且a<b<c,已知abc=3960,且a+b+c为偶数,则a+b+c=
50
50
.分析:把3960分解质因数:3960=2×2×2×5×9×11,由a+b+c为偶数,可得a,b,c有两个奇数一个偶数或三个都是偶数,然后即可求解.
解答:解:把3960分解质因数:3960=2×2×2×5×9×11,
∵a+b+c为偶数,∴a,b,c有两个奇数一个偶数或三个都是偶数,
若三个都是偶数则必是2的倍数,∴a=2×5=10,b=2×9=18,c=2×11=22,∴10+18+22=50;
若两个是奇数一个是偶数,则a=11,b=15,c=24,
∴11+15+24=50,
故答案为:50.
∵a+b+c为偶数,∴a,b,c有两个奇数一个偶数或三个都是偶数,
若三个都是偶数则必是2的倍数,∴a=2×5=10,b=2×9=18,c=2×11=22,∴10+18+22=50;
若两个是奇数一个是偶数,则a=11,b=15,c=24,
∴11+15+24=50,
故答案为:50.
点评:本题考查了整数的奇偶性,难度较大,关键是把3960分解质因数,然后分类讨论.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 名学生在五一期间去北京旅游,A旅行社的收费标准为:教师全价,学生半价;而B旅行社的收费标准为:不分教师、学生,一律八折优惠。已知这两家旅行社的基本价一样,都是每人500元。
名学生在五一期间去北京旅游,A旅行社的收费标准为:教师全价,学生半价;而B旅行社的收费标准为:不分教师、学生,一律八折优惠。已知这两家旅行社的基本价一样,都是每人500元。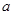 名学生在五一期间去北京旅游,A旅行社的收费标准为:教师全价,学生半价;而B旅行社的收费标准为:不分教师、学生,一律八折优惠。已知这两家旅行社的基本价一样,都是每人500元。
名学生在五一期间去北京旅游,A旅行社的收费标准为:教师全价,学生半价;而B旅行社的收费标准为:不分教师、学生,一律八折优惠。已知这两家旅行社的基本价一样,都是每人500元。