题目内容
某医院研制了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么在服药4h后血液含药量最高,达每毫升8微克,接着逐步衰减,10h 后血液中含药量为每毫升3微克.每毫升血液中含药量y(微克)随时间x(小时)的变化如图所示,当成人按规定剂量服药后.
后血液中含药量为每毫升3微克.每毫升血液中含药量y(微克)随时间x(小时)的变化如图所示,当成人按规定剂量服药后.
(1)分别求出当x≤4和x≥4时,y与x的函数关系式.
(2)如果每毫升含药4微克或4微克以上时在治疗上有效,则有效时间为多长?
解:(1)当x≤4时,设y=kx,
将(4,8)代入得:8=4k,
解得:k=2,
∴x≤4时,y与x的函数关系式为:y=2x;
当x≥4时,设y=kx+b,
∴ ,
,
解得: ,
,
∴当x≥4时,y与x的函数关系式为:y=- x+
x+ ;
;
(2)当y=4时,4=2x,解得:x1=2,
- x+
x+ =4,
=4,
解得:x2=8.8,
∴有效时间为:x2-x1=8.8-2=6.8(小时).
答:有效时间为6.8小时.
分析:(1)根据题意,观察图象,可得x≤44时,y与x的函数关系是正比例函数关系,x≥4时,y与x的函数关系是一次函数关系,然后根据待定系数法求解即可求得答案;
(2)观察图象,可知有效时间分别在两个函数上都有,所以分别求解,求其差即可求得答案.
点评:此题考查了一次函数的实际应用问题.此题难度适中,解题的关键是理解题意,读懂图象,注意数形结合思想的应用.
将(4,8)代入得:8=4k,
解得:k=2,
∴x≤4时,y与x的函数关系式为:y=2x;
当x≥4时,设y=kx+b,
∴
 ,
,解得:
 ,
,∴当x≥4时,y与x的函数关系式为:y=-
 x+
x+ ;
;(2)当y=4时,4=2x,解得:x1=2,
-
 x+
x+ =4,
=4,解得:x2=8.8,
∴有效时间为:x2-x1=8.8-2=6.8(小时).
答:有效时间为6.8小时.
分析:(1)根据题意,观察图象,可得x≤44时,y与x的函数关系是正比例函数关系,x≥4时,y与x的函数关系是一次函数关系,然后根据待定系数法求解即可求得答案;
(2)观察图象,可知有效时间分别在两个函数上都有,所以分别求解,求其差即可求得答案.
点评:此题考查了一次函数的实际应用问题.此题难度适中,解题的关键是理解题意,读懂图象,注意数形结合思想的应用.

练习册系列答案
相关题目
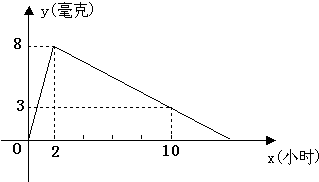 成人按剂量服药后
成人按剂量服药后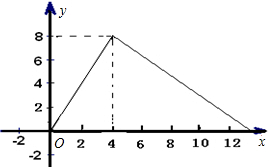 后血液中含药量为每毫升3微克.每毫升血液中含药量y(微克)随时间x(小时)的变化如图所示,当成人按规定剂量服药后.
后血液中含药量为每毫升3微克.每毫升血液中含药量y(微克)随时间x(小时)的变化如图所示,当成人按规定剂量服药后.
