题目内容
【题目】在平面直角坐标系中,直线y=2x+4与两坐标轴分别交于A,B两点.
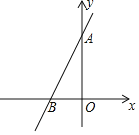
(1)若一次函数y=﹣![]() x+m与直线AB的交点在第二象限,求m的取值范围;
x+m与直线AB的交点在第二象限,求m的取值范围;
(2)若M是y轴上一点,N是x轴上一点,直线AB上是否存在两点P,Q,使得以M,N,P,Q四点为顶点的四边形是正方形.若存在,求出M,N两点的坐标,若不存在,请说明理由.
【答案】(1)m<4;(2)M(0,![]() ),N(﹣
),N(﹣![]() ,0)或M(0,﹣
,0)或M(0,﹣![]() ),N(
),N(![]() ,0)或M(0,﹣4),N(﹣
,0)或M(0,﹣4),N(﹣![]() ,0);
,0);
【解析】
(1)根据题意联立一次函数解析式与直线AB的解析式,据此进一步用![]() 表示出
表示出![]() ,最后根据第二象限的点的坐标特征加以分析即可;
,最后根据第二象限的点的坐标特征加以分析即可;
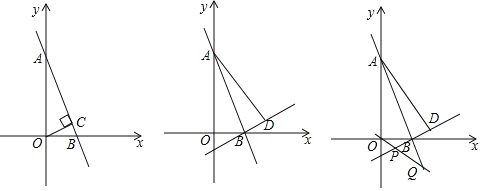
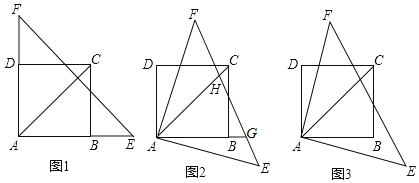
(2)首先求出A、B两点坐标,然后根据题意分图1、图2、图3共三种情况结合相似三角形性质进一步分析求解即可.
(1)联立![]() 与
与![]() ,得:
,得:![]() ,
,
∴![]() ,
,
∵交点位于第二象限,
∴![]() ,
,
∴![]() ;
;
(2)当![]() 时,
时,![]() ,
,
∴A(0,4),
当![]() 时,
时,![]() ,即:
,即:![]() ,
,
∴B(![]() ,0),
,0),
∴OA=4,OB=2.

如图1,过点Q作QH⊥![]() 轴于H,
轴于H,
∵MN∥AB,
∴△NMO~△BAO,
∴![]() ,
,
设ON=![]() ,则OM=
,则OM=![]() ,
,
∵∠MNQ=90°,
∴∠QNH+∠MNO=∠MNO+∠NMO=90°,
∴∠QNH=∠NMO,
在△QNH和△NMO中,
∵∠QNH=∠NMO,∠QHN=∠NOM,QN=MN,
∴△QNH△NMO(AAS),
∴QH=ON=![]() ,HN=OM=2
,HN=OM=2![]() ,
,
易得:△BQH~△BAO,
∴![]() ,
,
∴BH=![]() ,
,
∵OB=BH+HN+ON,
∴2=![]() ,解得
,解得![]() ,
,
∴M(0,![]() ),N(
),N(![]() ,0);
,0);
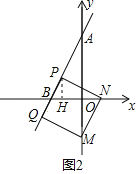
如图2,过点P作PH⊥![]() 轴于H,
轴于H,
易证△PNH~△BAO,
∴![]() ,
,
设PH=b,则NH=2b,
同理证得△PNH△NMO,
∴PH=ON=b,HN=OM=2b,
∴OH=HNOH=b,
易得:△BPH~△BAO,
∴![]() ,
,
∴BH=![]() b,
b,
∵OB=BH+OH,
∴2=![]() b+b,解得b=
b+b,解得b=![]() ,
,
∴M(0,![]() ),N(
),N(,0);
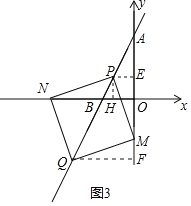
如图3,过点P作PH⊥![]() 轴于H,PE⊥y轴于E,QF⊥y轴于F,
轴于H,PE⊥y轴于E,QF⊥y轴于F,
易得:△PAE~△BAO,
∴![]() ,
,
设PE=c,则AE=2c,
同理证得△PNH△PME,
∴PH=PE=OE=c,则AE=2c,
∵OA=AE+OE,
∴4=2c+c,解得c=![]() ,
,
∵△MQF△PME,
∴MF=PE=OE,EM=FQ,
∴EM=OF=FQ,设EM=OF=FQ=m,
则Q(﹣m,﹣m),代入y=2x+4中,得﹣m=﹣2m+4,解得m=4,
∴NO=NH+OH=![]() ,∴N(
,∴N(![]() ,0),
,0),
∵OF=m=4,
∴M(0,﹣4).
综上所述M(0,![]() ),N(
),N(![]() ,0)或M(0,
,0)或M(0,![]() ),N(
),N(![]() ,0)或M(0,﹣4),N(
,0)或M(0,﹣4),N(![]() ,0).
,0).

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案