题目内容
(2010•邢台二模)如图,在菱形ABCD中,AB=10,∠ABC=60°.点Q从点D出发沿折线DC→CA→AB以每秒3个单位长的速度匀速运动;点P从点B沿BC以每秒1个单位长的速度匀速运动,射线PK随点P移动,保持与BC垂直,且交折线AB-AC于点E,交直线AD于点F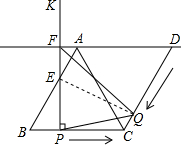 ,当点Q运动到点B时,停止运动,点P也随之停止.P、Q两点同时出发,设Q运动的时间为t(s).
,当点Q运动到点B时,停止运动,点P也随之停止.P、Q两点同时出发,设Q运动的时间为t(s).
(1)当t为何值时,BP=AF?
(2)当t为何值时,QE⊥AB?
(3)设直线PK扫过菱形ABCD的面积为S,试求S和t之间的函数关系式;
(4)当Q在线段CD上运动时,请直接写出△PQF为等腰三角形时t的值.
 ,当点Q运动到点B时,停止运动,点P也随之停止.P、Q两点同时出发,设Q运动的时间为t(s).
,当点Q运动到点B时,停止运动,点P也随之停止.P、Q两点同时出发,设Q运动的时间为t(s).(1)当t为何值时,BP=AF?
(2)当t为何值时,QE⊥AB?
(3)设直线PK扫过菱形ABCD的面积为S,试求S和t之间的函数关系式;
(4)当Q在线段CD上运动时,请直接写出△PQF为等腰三角形时t的值.
分析:(1)当E是AB的中点时,AF=BP,根据PF⊥BC,∠ABC=60°,可求解.
(2)当Q在CD上,AC上,AB上运动时,根据不同情况求出解.
(3)开始扫过的是三角形的面积,以后扫过的是四边形的面积,根据面积公式可求出函数式.
(4)两边相等的三角形是等腰三角形,根据此可求出解.
(2)当Q在CD上,AC上,AB上运动时,根据不同情况求出解.
(3)开始扫过的是三角形的面积,以后扫过的是四边形的面积,根据面积公式可求出函数式.
(4)两边相等的三角形是等腰三角形,根据此可求出解.
解答:解:(1)∵PF⊥BC,∠ABC=60°,AB=10,
∴PF=5
,
∵E为PF的中点,
∴PE=
,
∴BP=
,
∴t=
.
(2)当点Q在DC上时,
3t-5=10-2t
t=3.
当点Q在AC上运动时,不可能.
当Q在AB上运动时,
10-(10-t)-(3t-20)=5
t=7.5.
(3)在前5秒钟内,BP=t,PE=
t,
∴S=
t2(0≤t≤5).
在5秒后运动时,扫过的面积是梯形,
S=
(t-5+t)5
=5
t-
.
(4)△PQF为等腰三角形时,t=
,
.
∴PF=5
| 3 |
∵E为PF的中点,
∴PE=
5
| ||
| 2 |
∴BP=
| 5 |
| 2 |
∴t=
| 5 |
| 2 |
(2)当点Q在DC上时,
3t-5=10-2t
t=3.
当点Q在AC上运动时,不可能.
当Q在AB上运动时,
10-(10-t)-(3t-20)=5
t=7.5.
(3)在前5秒钟内,BP=t,PE=
| 3 |
∴S=
| ||
| 2 |
在5秒后运动时,扫过的面积是梯形,
S=
| 1 |
| 2 |
| 3 |
| 3 |
| 25 |
| 2 |
| 3 |
(4)△PQF为等腰三角形时,t=
| 5 |
| 3 |
60-15
| ||
| 13 |
点评:本题考查了菱形的性质,菱形的四边相等,等腰三角形的判定以及全等三角形的判定和性质.

练习册系列答案
相关题目
 (2010•邢台二模)如图,已知⊙O的直径AB与弦AC的夹角为31°,过C点的切线PC与AB的延长线交于点P,则∠P等于( )
(2010•邢台二模)如图,已知⊙O的直径AB与弦AC的夹角为31°,过C点的切线PC与AB的延长线交于点P,则∠P等于( )