题目内容
已知△ABC中,点E为边AB的中点,将△ABC沿CE所在的直线折叠得△AEC,BF∥AC,交直线A′C于F.
(1)若∠ACB=90°,∠A=30°,求证:AC=CF+BF.
(2)若∠ACB为任意角,在图(2)图(3)的情况下分别写出AC、CF、BF之间关系,并证明图(3)结论.
(3)如图(4),若∠ACB=120°,BF=6,BC=4,则AC的长为

(1)若∠ACB=90°,∠A=30°,求证:AC=CF+BF.
(2)若∠ACB为任意角,在图(2)图(3)的情况下分别写出AC、CF、BF之间关系,并证明图(3)结论.
(3)如图(4),若∠ACB=120°,BF=6,BC=4,则AC的长为
6+2
| 7 |
6+2
.| 7 |

分析:(1)根据直角三角形斜边上的中线等于斜边的一半可得AE=CE,根据等边对等角可得∠ACE=∠A,再根据翻折的性质可得∠A′CE=∠ACE,然后求出∠BCF=30°,再根据两直线平行,同旁内角互补求出∠CBF=90°,然后用BF表示出CF、BC,再表示出AC,即可得证;
(2)图(2),连接A′B,根据翻折的性质可得A′E=AE,A′C=AC,∠A=∠CA′E,根据中点定义可得AE=BE,从而得到BE=A′E,然后根据等边对等角可得∠EA′B=∠EBA′,根据两直线平行,内错角相等可得∠A=∠ABF,然后求出∠FA′B=∠FBA′,根据等角对等边可得A′F=BF,再根据A′C=CF+A′F整理即可得证;图(3)同理求出A′F=BF,再根据A′C=CF-A′F整理即可得证;
(3)连接A′B,过点F作FG⊥BC于G,根据两直线平行,同旁内角互补求出∠CBF=60°,然后解直角三角形求出BG、FG,再求出CG,然后利用勾股定理列式求出CF,再根据AC=CF+BF代入数据计算即可得解.
(2)图(2),连接A′B,根据翻折的性质可得A′E=AE,A′C=AC,∠A=∠CA′E,根据中点定义可得AE=BE,从而得到BE=A′E,然后根据等边对等角可得∠EA′B=∠EBA′,根据两直线平行,内错角相等可得∠A=∠ABF,然后求出∠FA′B=∠FBA′,根据等角对等边可得A′F=BF,再根据A′C=CF+A′F整理即可得证;图(3)同理求出A′F=BF,再根据A′C=CF-A′F整理即可得证;
(3)连接A′B,过点F作FG⊥BC于G,根据两直线平行,同旁内角互补求出∠CBF=60°,然后解直角三角形求出BG、FG,再求出CG,然后利用勾股定理列式求出CF,再根据AC=CF+BF代入数据计算即可得解.
解答:(1)证明:∵∠ACB=90°,点E为边AB的中点,
∴AE=CE,
∴∠ACE=∠A=30°,
由翻折的性质得,∠A′CE=∠ACE,
∴∠BCF=90°-30°×2=30°,
∵BF∥AC,
∴∠CBF=180°-∠ACB=180°-90°=90°,
∴CF=2BF,BC=BF÷tan30°=BF÷
=
BF,
又∵AC=BC÷tan30°=
BF÷
=3BF,
∴AC=CF+BF;
(2)解:如图(2),连接A′B,
由翻折的性质得,A′E=AE,A′C=AC,∠A=∠CA′E,
∵点E为边AB的中点,
∴AE=BE,
∴BE=A′E,
∴∠EA′B=∠EBA′,
∵BF∥AC,
∴∠A=∠ABF,
∵∠FA′B=∠EA′B-∠CA′E,
∠FBA′=∠EBA′-∠ABF,
即∠FA′B=∠FBA′,
∴A′F=BF,
∵A′C=CF+A′F,
∴AC=CF+BF;
如图(3),连接A′B,
由翻折的性质得,A′E=AE,A′C=AC,∠A=∠CA′E,
∵点E为边AB的中点,
∴AE=BE,
∴BE=A′E,
∴∠EA′B=∠EBA′,
∵BF∥AC,
∴∠A+∠ABF=180°,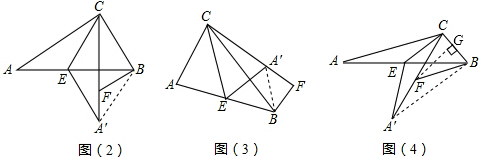
∵∠CA′E+∠EA′F=180°,
∴∠ABF=∠EA′F,
∵∠FA′B=∠EA′F-∠EA′B,
∠FBA′=∠ABF-∠EBA′,
即∠FA′B=∠FBA′,
∴A′F=BF,
∵A′C=CF-A′F,
∴AC=CF-BF;
(3)解:如图(4),连接A′B,过点F作FG⊥BC于G,
∵BF∥AC,∠ACB=120°,
∴∠CBF=180°-120°=60°,
∴BG=BF•cos60°=6×
=3,FG=BF•sin60°=6×
=3
,
∴CG=BC-BG=4-3=1,
在Rt△CGF中,CF=
=
=2
,
∴AC=BF+CF=6+2
.
故答案为:6+2
.
∴AE=CE,
∴∠ACE=∠A=30°,
由翻折的性质得,∠A′CE=∠ACE,
∴∠BCF=90°-30°×2=30°,
∵BF∥AC,
∴∠CBF=180°-∠ACB=180°-90°=90°,
∴CF=2BF,BC=BF÷tan30°=BF÷
| ||
| 3 |
| 3 |
又∵AC=BC÷tan30°=
| 3 |
| ||
| 3 |
∴AC=CF+BF;
(2)解:如图(2),连接A′B,
由翻折的性质得,A′E=AE,A′C=AC,∠A=∠CA′E,
∵点E为边AB的中点,
∴AE=BE,
∴BE=A′E,
∴∠EA′B=∠EBA′,
∵BF∥AC,
∴∠A=∠ABF,
∵∠FA′B=∠EA′B-∠CA′E,
∠FBA′=∠EBA′-∠ABF,
即∠FA′B=∠FBA′,
∴A′F=BF,
∵A′C=CF+A′F,
∴AC=CF+BF;
如图(3),连接A′B,
由翻折的性质得,A′E=AE,A′C=AC,∠A=∠CA′E,
∵点E为边AB的中点,
∴AE=BE,
∴BE=A′E,
∴∠EA′B=∠EBA′,
∵BF∥AC,
∴∠A+∠ABF=180°,

∵∠CA′E+∠EA′F=180°,
∴∠ABF=∠EA′F,
∵∠FA′B=∠EA′F-∠EA′B,
∠FBA′=∠ABF-∠EBA′,
即∠FA′B=∠FBA′,
∴A′F=BF,
∵A′C=CF-A′F,
∴AC=CF-BF;
(3)解:如图(4),连接A′B,过点F作FG⊥BC于G,
∵BF∥AC,∠ACB=120°,
∴∠CBF=180°-120°=60°,
∴BG=BF•cos60°=6×
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴CG=BC-BG=4-3=1,
在Rt△CGF中,CF=
| FG2+CG2 |
(3
|
| 7 |
∴AC=BF+CF=6+2
| 7 |
故答案为:6+2
| 7 |
点评:本题考查了翻折变换,平行线的性质,等边对等角的性质,解直角三角形,勾股定理的应用,作辅助线构造出等腰三角形是解题的关键,也是本题的难点.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
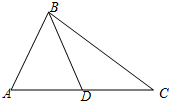 如图,已知△ABC中,点D为边AC的中点,设
如图,已知△ABC中,点D为边AC的中点,设 19、如图,已知△ABC中,点F是BC的中点,DE∥BC,则DG和GE有怎样的关系?请你说明理由.
19、如图,已知△ABC中,点F是BC的中点,DE∥BC,则DG和GE有怎样的关系?请你说明理由. 22、如图,已知△ABC中,点D、E在BC上,AB=AC,AD=AE.请说明BD=CE的理由.
22、如图,已知△ABC中,点D、E在BC上,AB=AC,AD=AE.请说明BD=CE的理由.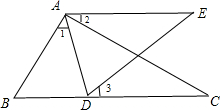 如图所示,已知△ABC中,点D为BC边上一点,∠1=∠2=∠3,AC=AE,
如图所示,已知△ABC中,点D为BC边上一点,∠1=∠2=∠3,AC=AE,