题目内容
以下列命题中正确的是
①x=1是不等式-2x<1的解;
②已知多项式2x2+bx+c分解因式为2(x-3)(x+1),则b=-4,c=-6;
③已知关于x的不等式组
的解集为3≤x<5,则
的值为-4;
④如果把
中的x和y都扩大5倍,那么分式的值不变.
①②④
①②④
(填命题的编号).①x=1是不等式-2x<1的解;
②已知多项式2x2+bx+c分解因式为2(x-3)(x+1),则b=-4,c=-6;
③已知关于x的不等式组
|
| b |
| a |
④如果把
| 2y |
| 2x-3y |
分析:①把x=1代入进行检验即可;
②2(x-3)(x+1)=2x2-4x-6,根据多项式相等的条件:对应项的系数相同,即可求得b,c的值;
③首先解不等式组,根据不等式组的解集即可得到一个关于a,b的方程组,求得a,b的值,进而求得
的值;
⑤用6x代替式子中的x,6y代替式子中的y,然后对所得的式子进行化简即可.
②2(x-3)(x+1)=2x2-4x-6,根据多项式相等的条件:对应项的系数相同,即可求得b,c的值;
③首先解不等式组,根据不等式组的解集即可得到一个关于a,b的方程组,求得a,b的值,进而求得
| b |
| a |
⑤用6x代替式子中的x,6y代替式子中的y,然后对所得的式子进行化简即可.
解答:解:①把x=1代入不等式,成立,故命题正确;
②2(x-3)(x+1)=2x2-4x-6=2x2+bx+c,则b=-4,c=-6,故命题正确;
③解不等式组
,
解①得:x≥a+b,
解②得:x<
.
根据题意得:
,
解得:
,则
=-2,故命题错误;
④用6x代替式子中的x,6y代替式子中的y.
则
=
,故式子的值不变,故命题正确.
则正确的是:①②④.
故答案是:①②④.
②2(x-3)(x+1)=2x2-4x-6=2x2+bx+c,则b=-4,c=-6,故命题正确;
③解不等式组
|
解①得:x≥a+b,
解②得:x<
| a+2b+1 |
| 2 |
根据题意得:
|
解得:
|
| b |
| a |
④用6x代替式子中的x,6y代替式子中的y.
则
| 12x |
| 12x-18y |
| 2y |
| 2x-3y |
则正确的是:①②④.
故答案是:①②④.
点评:主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题,解题的关键是正确理解不等式组的解的定义,以及解集的确定方法,分式的性质.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 是不等式
是不等式 的解;
的解; 的解集为
的解集为 ,则
,则  ;
; 中的x和y都扩大5倍,那么分式的值不变。
中的x和y都扩大5倍,那么分式的值不变。 是不等式
是不等式 的解;
的解; 分解因式为
分解因式为 ,则
,则 ;
; 的解集为
的解集为 ,则
,则 的值为
的值为 ;
; 中的x和y都扩大5倍,那么分式的值不变。
中的x和y都扩大5倍,那么分式的值不变。 是不等式
是不等式 的解;
的解; 分解因式为
分解因式为 ,则
,则 ;
;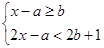 的解集为
的解集为 ,则
,则  的值为
的值为 ;
; 中的x和y都扩大5倍,那么分式的值不变。
中的x和y都扩大5倍,那么分式的值不变。 的解集为3≤x<5,则
的解集为3≤x<5,则  的值为-4;
的值为-4;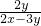 中的x和y都扩大5倍,那么分式的值不变.
中的x和y都扩大5倍,那么分式的值不变.