题目内容
已知不等式组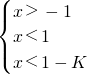
（1）分别求出当k=
，k=3，k=-2时不等式组的解集；
（2）由（1）可知不等式组的解集随k值的变化而变化，当k为任意实数时，写出不等式组的解集．
解：（1）当k=时，原不等式组可化为 
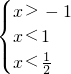，故不等式组的解集是-1＜x＜；
当k=3时，原不等式组可化为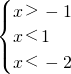
，故不等式组无解；
当k=-2时，原不等式组可化为
，故不等式组的解集是-1＜x＜1．
故答案为：-1＜x＜、无解、-1＜x＜1．
（2）若k为任意实数，不等式组的解集分以下三种情况：
当1-k≤-1即k≥2时，原不等式组可化为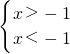
，故原不等式组的解集为无解；
当1-k≥1即k≤0时，原不等式组可化为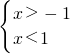
，故原不等式组的解集为-1＜x＜1；
当-1＜1-k＜1即0＜k＜2时，原不等式组可化为
，故原不等式组的解集为-1＜x＜1-k．
分析：（1）分别把k=，k=3，k=-2代入原不等式组，求出不等式组的公共解集即可；
（2）当k为任意有理数时，要分1-k＜-1，1-k＞1，-1＜1-k＜1三种情况分别求出不等式组的解集．
点评：本题考查的是不等式的解集，特别注意在解（2）时要分三种情况求不等式组的解集．
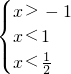时，原不等式组可化为 ，故不等式组的解集是-1＜x＜；当k=3时，原不等式组可化为
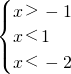，故不等式组无解；当k=-2时，原不等式组可化为
，故不等式组的解集是-1＜x＜1．故答案为：-1＜x＜
、无解、-1＜x＜1．（2）若k为任意实数，不等式组的解集分以下三种情况：
当1-k≤-1即k≥2时，原不等式组可化为
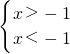，故原不等式组的解集为无解；当1-k≥1即k≤0时，原不等式组可化为
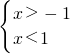，故原不等式组的解集为-1＜x＜1；当-1＜1-k＜1即0＜k＜2时，原不等式组可化为
，故原不等式组的解集为-1＜x＜1-k．分析：（1）分别把k=
，k=3，k=-2代入原不等式组，求出不等式组的公共解集即可；（2）当k为任意有理数时，要分1-k＜-1，1-k＞1，-1＜1-k＜1三种情况分别求出不等式组的解集．
点评：本题考查的是不等式的解集，特别注意在解（2）时要分三种情况求不等式组的解集．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南师范大学出版社系列答案
相关题目
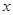＜0； ⑵ 
＜1； ⑶ 
； 
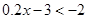．你喜欢其中哪两个不等式，请把它们选出来组成一个不等式组，求出它的解集，并在数轴上把解集表示出来．
＜0； ⑵ 
＜1； ⑶ 
； 
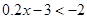．你喜欢其中哪两个不等式，请把它们选出来组成一个不等式组，求出它的解集，并在数轴上把解集表示出来．
＜1；⑶ 2x+3＞1；⑷ 0.2x－3＜－2.你喜欢其中哪两个不等式，请把它们选出来组成一个不等式组，求出它的解集，并在数轴上把解集表示出来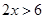
，
，
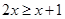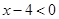，请从中选择你喜欢的两个不等式，组成一个不等式组，求出这个不等式组的解集，并把解集在数轴上表示出来．
，
，
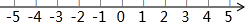
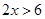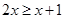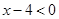，请从中选择你喜欢的两个不等式，组成一个不等式组，求出这个不等式组的解集，并把解集在数轴上表示出来．
