题目内容
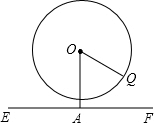 “国庆”期间,小李和同学一起到中山公园游玩大型摩天轮,摩天轮的半径为20m,匀速转动一周需要12min,小李乘座最底部的车厢(离地面1m),经过2min后到达Q点(如图所示),则此时他离地面的高度是( )
“国庆”期间,小李和同学一起到中山公园游玩大型摩天轮,摩天轮的半径为20m,匀速转动一周需要12min,小李乘座最底部的车厢(离地面1m),经过2min后到达Q点(如图所示),则此时他离地面的高度是( )| A、10m | ||
| B、11m | ||
C、10
| ||
D、(10
|
分析:先过Q作QB⊥EF,交EF于B,过Q作QC⊥AO于C,根据QB⊥EF,QC⊥AO,OA⊥EF,易证四边形ACQB是矩形,
从而有AC=BQ,又摩天轮转动一周需要12min,那么易求经过2min后到达Q点,所夹的∠AOQ的度数,在Rt△COQ中,易求∠CQO=30°,从而易求OC,进而可求AC,即得BQ.
从而有AC=BQ,又摩天轮转动一周需要12min,那么易求经过2min后到达Q点,所夹的∠AOQ的度数,在Rt△COQ中,易求∠CQO=30°,从而易求OC,进而可求AC,即得BQ.
解答: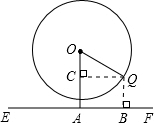 解:如右图所示,过Q作QB⊥EF,交EF于B,过Q作QC⊥AO于C,
解:如右图所示,过Q作QB⊥EF,交EF于B,过Q作QC⊥AO于C,
∵QB⊥EF,QC⊥AO,OA⊥EF,
∴∠ACQ=∠ABQ=∠OAB=90°,
∴四边形ACQB是矩形,
∴AC=BQ,
∵转动一周需要12min,
∴∠COQ=
×360°=60°,
∴∠CQO=30°,
∴OC=
OQ=10,
∴BQ=AC=OA-OC=20+1-10=11.
故选B.
 解:如右图所示,过Q作QB⊥EF,交EF于B,过Q作QC⊥AO于C,
解:如右图所示,过Q作QB⊥EF,交EF于B,过Q作QC⊥AO于C,∵QB⊥EF,QC⊥AO,OA⊥EF,
∴∠ACQ=∠ABQ=∠OAB=90°,
∴四边形ACQB是矩形,
∴AC=BQ,
∵转动一周需要12min,
∴∠COQ=
| 2 |
| 12 |
∴∠CQO=30°,
∴OC=
| 1 |
| 2 |
∴BQ=AC=OA-OC=20+1-10=11.
故选B.
点评:本题考查了矩形的判定和性质、特殊三角函数值、含有30°角的直角三角形的性质、圆心角、弧、弦的关系.解题的关键是作辅助线,求出∠COQ.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 “国庆”期间,小李和同学一起到中山公园游玩大型摩天轮,摩天轮的半径为20m,匀速转动一周需要12min,小李乘座最底部的车厢(离地面1m),经过2min后到达Q点(如图所示),则此时他离地面的高度是
“国庆”期间,小李和同学一起到中山公园游玩大型摩天轮,摩天轮的半径为20m,匀速转动一周需要12min,小李乘座最底部的车厢(离地面1m),经过2min后到达Q点(如图所示),则此时他离地面的高度是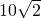 m
m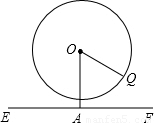
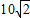 m
m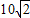 +1)m
+1)m