Question

（2004•青岛）如图，E，F，G，H分别是四边形ABCD四条边的中点，要使四边形EFGH为矩形，则四边形ABCD应具备的条件是（ ）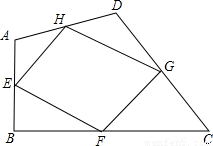

A．一组对边平行而另一组对边不平行
B．对角线相等
C．对角线互相垂直
D．对角线互相平分

Answer 1

【答案】分析：根据三角形的中位线定理得到四边形EFGH一定是平行四边形，再推出一个角是直角，由矩形的判定定理可求解．
解答：解：要是四边形EHGF是矩形，应添加条件是对角线互相垂直，
理由是：连接AC、BD，两线交于O，
根据三角形的中位线定理得：EF∥AC，EF=AC，GH∥AC，GH=AC，
∴EF∥GH，EF=GH，
∴四边形EFGH一定是平行四边形，
∴EF∥AC，EH∥BD，
∵BD⊥AC，
∴EH⊥EF，
∴∠HEF=90°，
故选C．
点评：能够根据三角形的中位线定理证明：顺次连接四边形各边中点所得四边形是平行四边形；顺次连接对角线互相垂直的四边形各边中点所得四边形是矩形；顺次连接对角线相等的四边形各边中点所得四边形是菱形．掌握这些结论，以便于运用．