题目内容
关于抛物线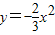 ,下列说法错误的是( )
,下列说法错误的是( )A.开口向下
B.对称轴是y轴
C.顶点是(0,0)
D.图象有最低点
【答案】分析:本题根据二次函数解析式,判断抛物线的有关性质.
解答:解:A、函数中a=- <0,开口向下,正确;
<0,开口向下,正确;
B、对称轴为x=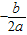 =0,即y轴,正确;
=0,即y轴,正确;
C、∵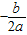 =0,
=0, =0,∴顶点坐标为(0,0),正确;
=0,∴顶点坐标为(0,0),正确;
D、图象有最高点,图象没有最低点.
故选D.
点评:主要考查了二次函数的性质以及对称轴和顶点坐标的求法.
解答:解:A、函数中a=-
 <0,开口向下,正确;
<0,开口向下,正确;B、对称轴为x=
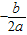 =0,即y轴,正确;
=0,即y轴,正确;C、∵
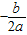 =0,
=0, =0,∴顶点坐标为(0,0),正确;
=0,∴顶点坐标为(0,0),正确;D、图象有最高点,图象没有最低点.
故选D.
点评:主要考查了二次函数的性质以及对称轴和顶点坐标的求法.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
.如图,关于抛物线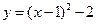 ,下列说法错误的是 ( )
,下列说法错误的是 ( )

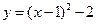 ,下列说法错误的是 ( )
,下列说法错误的是 ( )
A.顶点坐标为(1, ) ) |
| B.对称轴是直线x=l |
| C.开口方向向上 |
| D.当x>1时,Y随X的增大而减小 |
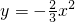 ,下列说法错误的是
,下列说法错误的是 ,下列说法错误的是 ( )
,下列说法错误的是 ( )
 )
) ,下列说法错误的是 ( )
,下列说法错误的是 ( ) A.顶点坐标为(1,
A.顶点坐标为(1, )
)