题目内容
（2003•桂林）如图，在直角坐标系中，有两个点A（4，0）、B（0，2），如果点C在x轴上（点C与点A不重合），当点C坐标为 时，使得由B、O、C三点组成的三角形和△AOB相似．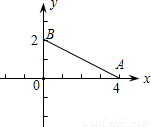
【答案】分析：本题可从两个三角形相似入手，根据c点在x轴上得知c点纵坐标为0，讨论OC与OA对应以及OC与OB对应的情况，分别讨论即可．
解答：解：∵点C在x轴上，
∴∠BOC=90°两个三角形相似时，应该与∠BOA=90°对应，
若OC与OA对应，则OC=OA=4，C（-4，0）；
若OC与OB对应，则OC=1，C（-1，0）或者（1，0）．
点评：首先判断由B、O、C三点组成的三角形形状，再利用两个三角形直角边与直角边对应关系的两种可能，分别求解．
解答：解：∵点C在x轴上，
∴∠BOC=90°两个三角形相似时，应该与∠BOA=90°对应，
若OC与OA对应，则OC=OA=4，C（-4，0）；
若OC与OB对应，则OC=1，C（-1，0）或者（1，0）．
点评：首先判断由B、O、C三点组成的三角形形状，再利用两个三角形直角边与直角边对应关系的两种可能，分别求解．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
上的动点（P与A、E点不重合），连接弦CP交EO2于F点，设CF=x，CP=y，求y与x的函数解析式，并确定自变量x的取值范围．
上的动点（P与A、E点不重合），连接弦CP交EO2于F点，设CF=x，CP=y，求y与x的函数解析式，并确定自变量x的取值范围．
