题目内容
某商场促销方案规定:商场内所有商品案标价的80%出售,同时,当顾客在商场内消费满一定金额后,按下表获得相应的返还金额。
注:300~400表示消费金额大于300元且小于或等于400元,其他类同。
根据上述促销方案,顾客在该商场购物可以获得双重优惠。例如,若购买标价为400元的商品,则消费金额为320元,获得的优惠额为400´(1-80%)+30=110(元)。
(1)购买一件标价为1000元的商品,顾客获得的优惠额是多少?
(2)如果顾客购买标价不超过800元的商品,要使获得的优惠额不少于226元,那么该商品的标价至少为多少元?
| 消费金额(元) | 300~400 | 400~500 | 500~600 | 600~700 | 700~900 | … |
| 返还金额(元) | 30 | 60 | 100 | 130 | 150 | … |
根据上述促销方案,顾客在该商场购物可以获得双重优惠。例如,若购买标价为400元的商品,则消费金额为320元,获得的优惠额为400´(1-80%)+30=110(元)。
(1)购买一件标价为1000元的商品,顾客获得的优惠额是多少?
(2)如果顾客购买标价不超过800元的商品,要使获得的优惠额不少于226元,那么该商品的标价至少为多少元?
(1)350(元)(2)630元
解:(1)∵购买一件标价为1000元的商品,消费金额为800元,
∴顾客获得的优惠额为1000´(1-80%)+150=350(元)。
(2)设该商品的标价为x元,
当80%x£500,即x£625时,顾客获得的优惠额不超过625´(1-80%)+60=185<226;
当500<80%x£600,即625£x£750时,(1-80%)x+100³226。解得x³630。所以630£x£750。
当600<80%x£800´80%,即750<x£800时,顾客获得的优惠额大于750´(1-80%)+130=280>226。
综上所述,顾客购买标价不超过800元的商品,要使获得的优惠额不少于226元,那么该商品的标价至少为630元。
(1)根据标价为1000元的商品按80%的价格出售,求出消费金额,再根据消费金额所在的范围,求出优惠额,从而得出顾客获得的优惠额。
(2)先设该商品的标价为x元,根据购买标价不超过800元的商品,要使获得的优惠不少于226元,分别情况列出不等式,求出x的取值范围,从而得出答案。
∴顾客获得的优惠额为1000´(1-80%)+150=350(元)。
(2)设该商品的标价为x元,
当80%x£500,即x£625时,顾客获得的优惠额不超过625´(1-80%)+60=185<226;
当500<80%x£600,即625£x£750时,(1-80%)x+100³226。解得x³630。所以630£x£750。
当600<80%x£800´80%,即750<x£800时,顾客获得的优惠额大于750´(1-80%)+130=280>226。
综上所述,顾客购买标价不超过800元的商品,要使获得的优惠额不少于226元,那么该商品的标价至少为630元。
(1)根据标价为1000元的商品按80%的价格出售,求出消费金额,再根据消费金额所在的范围,求出优惠额,从而得出顾客获得的优惠额。
(2)先设该商品的标价为x元,根据购买标价不超过800元的商品,要使获得的优惠不少于226元,分别情况列出不等式,求出x的取值范围,从而得出答案。

练习册系列答案
相关题目
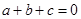 ,且
,且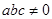 ,则
,则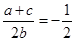
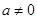 ,则
,则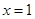 一定是方程
一定是方程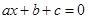 的解
的解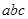 >0
>0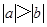 ,则
,则 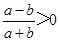
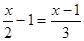 时,去分母正确的是( )
时,去分母正确的是( )



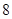 轮(即每个队均需要赛
轮(即每个队均需要赛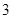 分,平一场得1分,负一场得
分,平一场得1分,负一场得 分.在这次足球联赛中,雄师队踢平的场数是所负场所的2倍,共得
分.在这次足球联赛中,雄师队踢平的场数是所负场所的2倍,共得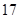 分.你知道雄师队胜了几场球吗?
分.你知道雄师队胜了几场球吗?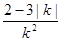 的值是 ( )
的值是 ( )


 2=
2= 2,那么
2,那么 >
>
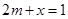 和方程
和方程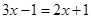 的解互为相反数,则m的值为( )
的解互为相反数,则m的值为( )