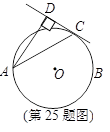
题目内容
（11·钦州）（本题满分12分）．如图，在平面直角坐标系中，抛物线与x轴交于A、B两点（A在B的左侧），与y轴交于点C (0，4)，顶点为
．
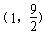（1）求抛物线的函数表达式；
（2）设抛物线的对称轴与轴交于点D，试在对称轴上找出点P，使△CDP为等腰三角形，请直接写出满足条件的所有点P的坐标．
（3）若点E是线段AB上的一个动点（与A、B不重合），分别连接AC、BC，过点E作EF∥AC交线段BC于点F，连接CE，记△CEF的面积为S，S是否存在最大值？若存在，求出S的最大值及此时E点的坐标；若不存在，请说明理由．
（1）∵抛物线的顶点为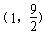
∴设抛物线的函数关系式为y＝a ( x－1) 2＋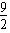
………………2分
∵抛物线与y轴交于点C (0，4)，
∴a (0－1) 2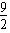＋＝4
解得a＝－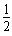
∴所求抛物线的函数关系式为y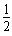＝－ ( x－1) 2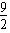＋ ………………4分
（2）解：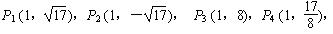
， ………………8分
（3）解：令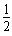－ ( x－1) 2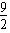＋＝0，解得x1＝－2，x1＝4
∴抛物线y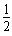＝－ ( x－1) 2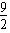＋与x轴的交点为A (－2，0) C (4，0)………………9分
过点F作FM⊥OB于点M，
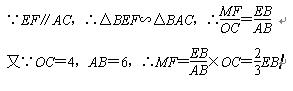
设E点坐标为 (x，0)，则EB＝4－x，MF＝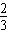
(4－x) …………10分
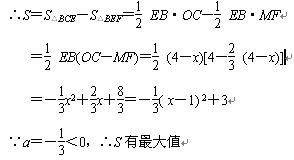
当x＝1时，S最大值＝3 …………11分
此时点E的坐标为 (1，0) …………12分解析:
略
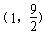
∴设抛物线的函数关系式为y＝a ( x－1) 2＋
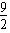………………2分∵抛物线与y轴交于点C (0，4)，
∴a (0－1) 2＋
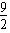＝4解得a＝－
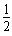
∴所求抛物线的函数关系式为y＝－
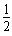( x－1) 2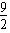＋ ………………4分（2）解：
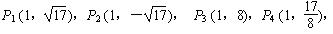， ………………8分（3）解：令－
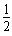( x－1) 2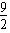＋＝0，解得x1＝－2，x1＝4∴抛物线y＝－
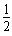( x－1) 2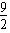＋与x轴的交点为A (－2，0) C (4，0)………………9分过点F作FM⊥OB于点M，
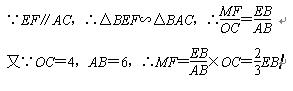
设E点坐标为 (x，0)，则EB＝4－x，MF＝
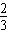(4－x) …………10分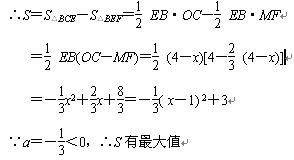当x＝1时，S最大值＝3 …………11分
此时点E的坐标为 (1，0) …………12分解析:
略
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
（11·钦州）（本题满分9分）
某校为了解九年级800名学生的体育综合素质，随机抽查了50名学生进行体育综合测试，所得成绩整理分成五组，并制成如下频数分布表和扇形统计图，请根据所提供的信息解答下列问题：
频数分布表 扇形统计图
| 组别 | 成绩（分） | 频数 |
| A | 50≤x＜60 | 3 |
| B | 60≤x＜80 | m |
| C | 70≤x＜80 | 10 |
| D | 80≤x＜90 | n |
| E | 90≤x＜100 | 15 |
（1）频数分布表中的m＝_ ▲ ，n＝_ ▲ ；
（2）样本中位数所在成绩的级别是_ ▲ ，扇形统计图中，E组所对应的扇形圆心角的度数是_ ▲ ；
（3）请你估计该校九年级的学生中，体育综合测试成绩不少于80分的大约有多少人？
