题目内容
有一个Rt△ABC,∠A=90°,∠B=60°,AB=1,将它放在平面直角坐标系中,使斜边BC在x轴上,直角顶点A在反比例函数y= 上,则点C的坐标为________.
上,则点C的坐标为________.
( ,0)(
,0)( ,0),(
,0),( ,0),(-
,0),(- ,0).
,0).
分析:由于反比例函数的图象是双曲线,点A可能在第一象限,也可能在第三象限,又因为斜边BC在x轴上,所以可能点B在点C的右边,也可能点B在点C的左边,故一共分四种情况.针对每一种情况,都可以运用三角函数的定义求出点C的坐标.
解答:

①当点A在第一象限时,如上图,
过点A作AD⊥x轴于D.
∵在Rt△ABD中,∠ADB=90°,∠ABC=60°,AB=1,
∴BD= ,AD=
,AD= ,
,
∵点A在反比例函数y= 上,
上,
∴当y= 时,x=2,∴A(2,
时,x=2,∴A(2, ),
),
在Rt△ACD中,∠ADC=90°,∠ACD=30°,AD= ,
,
∴CD= ,
,
∴OC=OD-CD=2- =
= ,
,
∴点C的坐标为( ,0);
,0);
②

当点A在第一象限时,如上图,
过点A作AD⊥x轴于D.
∵在Rt△ABD中,∠ADB=90°,∠ABC=60°,AB=1,
∴BD= ,AD=
,AD= ,
,
∵点A在反比例函数y= 上,
上,
∴当y= 时,x=2,∴A(2,
时,x=2,∴A(2, ),
),
在Rt△ACD中,∠ADC=90°,∠ACD=30°,AD= ,
,
∴CD= ,
,
∴OC=OD+CD=2+ =
= ,
,
∴点C的坐标为( ,0);
,0);
③

当点A在第三象限时,如上图,
过点A作AD⊥x轴于D.
∵在Rt△ABD中,∠ADB=90°,∠ABC=60°,AB=1,
∴BD= ,AD=
,AD= ,
,
∵点A在反比例函数y= 上,
上,
∴当y=- 时,x=-2,
时,x=-2,
∴A(-2,- ),
),
在Rt△ACD中,∠ADC=90°,∠ACD=30°,AD= ,
,
∴CD= ,
,
∴OC=OD-CD=2- =
= ,
,
∴点C的坐标为(- ,0);
,0);
④

当点A在第三象限时,如上图,
过点A作AD⊥x轴于D.
∵在Rt△ABD中,∠ADB=90°,∠ABC=60°,AB=1,
∴BD= ,AD=
,AD= ,
,
∵点A在反比例函数y= 上,
上,
∴当y=- 时,x=-2,
时,x=-2,
∴A(-2,- ),
),
在Rt△ACD中,∠ADC=90°,∠ACD=30°,AD= ,
,
∴CD= ,
,
∴OC=OD+CD=2+ =
= ,
,
∴点C的坐标为(- ,0).
,0).
综上,可知点C的坐标为
点评:本题考查反比例函数的综合运用以及30°角的直角三角形的性质,本题的关键是看到C的位置有4种不同的情况.
 ,0)(
,0)( ,0),(
,0),( ,0),(-
,0),(- ,0).
,0).分析:由于反比例函数的图象是双曲线,点A可能在第一象限,也可能在第三象限,又因为斜边BC在x轴上,所以可能点B在点C的右边,也可能点B在点C的左边,故一共分四种情况.针对每一种情况,都可以运用三角函数的定义求出点C的坐标.
解答:

①当点A在第一象限时,如上图,
过点A作AD⊥x轴于D.
∵在Rt△ABD中,∠ADB=90°,∠ABC=60°,AB=1,
∴BD=
 ,AD=
,AD= ,
,∵点A在反比例函数y=
 上,
上,∴当y=
 时,x=2,∴A(2,
时,x=2,∴A(2, ),
),在Rt△ACD中,∠ADC=90°,∠ACD=30°,AD=
 ,
,∴CD=
 ,
,∴OC=OD-CD=2-
 =
= ,
,∴点C的坐标为(
 ,0);
,0);②

当点A在第一象限时,如上图,
过点A作AD⊥x轴于D.
∵在Rt△ABD中,∠ADB=90°,∠ABC=60°,AB=1,
∴BD=
 ,AD=
,AD= ,
,∵点A在反比例函数y=
 上,
上,∴当y=
 时,x=2,∴A(2,
时,x=2,∴A(2, ),
),在Rt△ACD中,∠ADC=90°,∠ACD=30°,AD=
 ,
,∴CD=
 ,
,∴OC=OD+CD=2+
 =
= ,
,∴点C的坐标为(
 ,0);
,0);③

当点A在第三象限时,如上图,
过点A作AD⊥x轴于D.
∵在Rt△ABD中,∠ADB=90°,∠ABC=60°,AB=1,
∴BD=
 ,AD=
,AD= ,
,∵点A在反比例函数y=
 上,
上,∴当y=-
 时,x=-2,
时,x=-2,∴A(-2,-
 ),
),在Rt△ACD中,∠ADC=90°,∠ACD=30°,AD=
 ,
,∴CD=
 ,
,∴OC=OD-CD=2-
 =
= ,
,∴点C的坐标为(-
 ,0);
,0);④

当点A在第三象限时,如上图,
过点A作AD⊥x轴于D.
∵在Rt△ABD中,∠ADB=90°,∠ABC=60°,AB=1,
∴BD=
 ,AD=
,AD= ,
,∵点A在反比例函数y=
 上,
上,∴当y=-
 时,x=-2,
时,x=-2,∴A(-2,-
 ),
),在Rt△ACD中,∠ADC=90°,∠ACD=30°,AD=
 ,
,∴CD=
 ,
,∴OC=OD+CD=2+
 =
= ,
,∴点C的坐标为(-
 ,0).
,0).综上,可知点C的坐标为

点评:本题考查反比例函数的综合运用以及30°角的直角三角形的性质,本题的关键是看到C的位置有4种不同的情况.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 相切,求m的值.
相切,求m的值. 如图,在12×6的网格中(每个小正方形的边长均为1个单位长),有一个Rt△ABC和一个半圆O(A、B、C、O均为格点),∠C=90°,半圆O的半径为2.将Rt△ABC沿AC方向向右平移m个单位,使其斜边恰好与半圆O相切,求m的值.
如图,在12×6的网格中(每个小正方形的边长均为1个单位长),有一个Rt△ABC和一个半圆O(A、B、C、O均为格点),∠C=90°,半圆O的半径为2.将Rt△ABC沿AC方向向右平移m个单位,使其斜边恰好与半圆O相切,求m的值. 有一个Rt△ABC,∠A=90°,∠B=60°,AB=1,将它放在如图直角坐标系中,使斜边BC在x轴上,直角顶点A在反比例函数y=-
有一个Rt△ABC,∠A=90°,∠B=60°,AB=1,将它放在如图直角坐标系中,使斜边BC在x轴上,直角顶点A在反比例函数y=-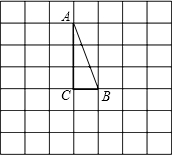 在如图的方格纸中有一个Rt△ABC(A、B、C三点均为格点),∠C=90°.现将Rt△ABC绕点B顺时针旋转90°后所得到的Rt△A′BC'.
在如图的方格纸中有一个Rt△ABC(A、B、C三点均为格点),∠C=90°.现将Rt△ABC绕点B顺时针旋转90°后所得到的Rt△A′BC'.