题目内容
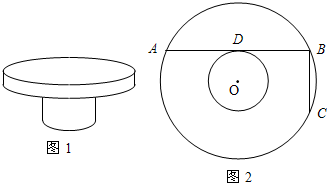
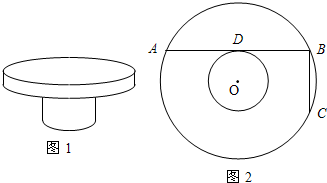
图1是一个机器零件的立体示意图，为了求出这个零件大小两个同心圆柱的半径，陈华用曲尺在大圆柱的背面上画了两条互相垂直的弦AB、BC，如图2所示，其中AB⊥BC，AB与小圆相切于点D，已知量得AB=12cm，BC=5cm，分别求这两个圆的半径．
【答案】分析：根据勾股定理得出AC的长，再利用切线的性质定理得出DO=
BC即可得出答案．
解答：
解：连接AC，DO，
∵AB⊥BC，AB=12cm，BC=5cm，
∴AC=13，
∴大圆的半径为：6.5．
∵AB与小圆相切于点D，
∴DO⊥AB，
∴DO∥BC，
AO=CO，
∴DO=
BC=2.5，
∴小圆的半径为：2.5．
点评：此题主要考查了切线的性质定理以及勾股定理等知识，根据已知得出DO=
BC是解决问题的关键．
BC即可得出答案．解答：
解：连接AC，DO，∵AB⊥BC，AB=12cm，BC=5cm，
∴AC=13，
∴大圆的半径为：6.5．
∵AB与小圆相切于点D，
∴DO⊥AB，
∴DO∥BC，
AO=CO，
∴DO=
BC=2.5，∴小圆的半径为：2.5．
点评：此题主要考查了切线的性质定理以及勾股定理等知识，根据已知得出DO=
BC是解决问题的关键． 
练习册系列答案
相关题目
