题目内容
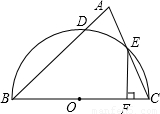
(2002•内江)如图,以△ABC的BC边为直径的半圆交AB于D,交AC于E,EF⊥BC,垂足为F,BF:FC=5:1,AB=8cm,AE=2cm.则AD的长是 cm.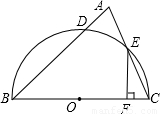
【答案】分析:由割线定理知:AD•AB=AE•AC,因此求AD的长,缺少的是AC或EC的长;可通过构建直角三角形求解.连接BE,在Rt△ABE中,BE的长可由勾股定理求得;在Rt△BEC中,EF⊥BC,根据射影定理可得BE2=BF•FC,由此可求出FC、BC的长,进而可求出EC的长;即可得AD的长.
解答: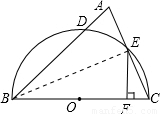 解:连接BE,则∠BEC=90°;
解:连接BE,则∠BEC=90°;
在Rt△AEB中,AB=8cm,AE=2cm;由勾股定理得,BE2=60.
在Rt△BEC中,EF⊥BC,根据射影定理,可得:
BE2=BF•BC=5FC•6FC=30FC2;
∵BE2=60,∴FC=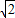 cm,BC=6
cm,BC=6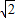 cm;
cm;
同理,可得:EC2=FC•BC=12,即EC=2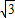 cm.
cm.
由割线定理,得:AD•AB=AE•AC,即:
AD×8=2×(2+2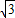 ),解得AD=
),解得AD=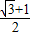 cm.
cm.
点评:本题考查了圆周角定理、直角三角形的性质、相似三角形的性质、勾股定理等知识的综合应用.
解答:
 解:连接BE,则∠BEC=90°;
解:连接BE,则∠BEC=90°;在Rt△AEB中,AB=8cm,AE=2cm;由勾股定理得,BE2=60.
在Rt△BEC中,EF⊥BC,根据射影定理,可得:
BE2=BF•BC=5FC•6FC=30FC2;
∵BE2=60,∴FC=
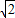 cm,BC=6
cm,BC=6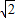 cm;
cm;同理,可得:EC2=FC•BC=12,即EC=2
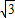 cm.
cm.由割线定理,得:AD•AB=AE•AC,即:
AD×8=2×(2+2
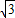 ),解得AD=
),解得AD=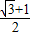 cm.
cm.点评:本题考查了圆周角定理、直角三角形的性质、相似三角形的性质、勾股定理等知识的综合应用.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 时求此抛物线的解析式;
时求此抛物线的解析式;
 时求此抛物线的解析式;
时求此抛物线的解析式;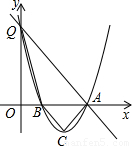
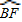 上一点,且
上一点,且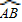 =
=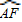 ,AD⊥BC,垂足为D,过A作AE∥BF交CB的延长线于E.
,AD⊥BC,垂足为D,过A作AE∥BF交CB的延长线于E. ;
; .
.