题目内容
一根弹簧的原长为12 cm，它能挂的重量不能超过15 kg并且每挂重1kg就伸长cm写出挂重后的弹簧长度y（cm）与挂重x（kg）之间的函数关系式是（ ）
| A．y = x + 12（0＜x≤15） | B．y = x + 12 （0≤x＜15） |
| C．y = x + 12（0≤x≤15） | D．y = x + 12 （0＜x＜15） |
C
根据函数的概念：函数中的每个值x，变量y按照一定的法则有一个确定的值y与之对应，解答即可：设挂重为x，则弹簧伸长为x，
挂重后弹簧长度y（cm）与挂重x（kg）之间的函数关系式是：y=x+12 （0≤x≤15）．
故选C．
挂重后弹簧长度y（cm）与挂重x（kg）之间的函数关系式是：y=x+12 （0≤x≤15）．
故选C．
练习册系列答案
相关题目
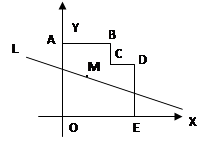
解的情况为__________________.
、线段
分别表示甲、乙两车所行路程
（千米）与时间
（小时）之间的函数关系对应的图象（线段
表示甲出发不足2小时因故停车检修）．请根据图象所提供的信息，解决如下问题：
与反比例函数
的图象相交于点
、
，
与
轴交于点
，其中点
，点
.
的面积.
与
(小时)之间的关系. 
与