题目内容
如图,已知平面直角坐标系xOy中的点A(0,1),B(1,0),M、N为线段AB上两动点,过点M作x轴的平行线交y轴于点E,过点N作y轴的平行线交x轴于点F,交直线EM于点P(x,y),且S△MPN=S△AEM+S△NFB.
(1)S△AOB______S矩形EOFP(填“>”、“=”、“<”),y与x的函数关系是______(不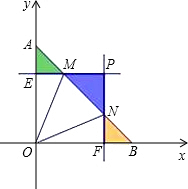 要求写自变量的取值范围);
要求写自变量的取值范围);
(2)当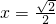 时,求∠MON的度数;
时,求∠MON的度数;
(3)证明:∠MON的度数为定值.
解:(1)∵S△MPN=S△AEM+S△NFB.
∴S△AOB=S矩形EOFP;
∵S△AOB= OA•OB=
OA•OB= ×1×1=
×1×1= ,
,
∴S矩形EOFP= ,
,
∴y与x的函数关系是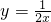 ;
;
(2)当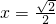 时,
时, ,∴点P的坐标为
,∴点P的坐标为 .
.
可得四边形EOFP为正方形,过点O作OH⊥AB于H,
∵在Rt△AOB中,OA=OB=1,
∴ ,H为AB的中点,
,H为AB的中点,
∴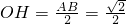 .
.
在Rt△EMO和Rt△HMO中,
∴Rt△EMO≌Rt△HMO.
∴∠1=∠2.
同理可证∠3=∠4.
∵∠1+∠2+∠3+∠4=90°,
∴∠2+∠3=45°.
即∠MON=45°.
(3)过点O作OH⊥AB于H,
依题意,可得 ,
,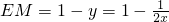 ,
,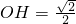 ,
,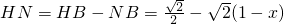 ,
,
∴ ,∠OEM=∠OHN=90°,
,∠OEM=∠OHN=90°,
∴△EMO∽△HNO,
∴∠1=∠3.
同理可证∠2=∠4,
∵∠1+∠2+∠3+∠4=90°,
∴∠2+∠3=45°即∠MON=45°.
分析:(1)由于△AOB与矩形EOFP有公共部分五边形OEMNF,而不同的部分是△AEM、△BFN和△PMN,若比较△AOB和矩形EOFP的面积大小,只需比较不同部分的面积大小即可,由已知得S△MPN=S△AEM+S△NFB,故两者的面积相等;y与x的函数关系:可根据P点坐标,求出矩形EPFO的面积,根据△AOB和矩形的面积相等,即可得到关于x、y的函数关系式;
(2)将x的值代入题(1)所得的函数关系式中,即可得到y的值,也就确定了P点的坐标;过O作OH⊥AB于H,在等腰Rt△OAB中,通过解直角三角形,可求得AB、OH的长,此时发现OH=OE,则可证得Rt△EMO≌Rt△HMO,由此可得∠1=∠2,同理可证得∠3=∠4,由于∠EOF=90°,则∠2+∠3=∠MON=45°,由此得解.
(3)方法同(2)类似,可用P点的横坐标,分别表示出EM、HN的长,通过证△EMO∽△HNO,得到∠1=∠3,同理可通过证△MHO∽△NFO,得到∠2=∠4,而∠EOF=90°,即可得到∠MON=45°.
点评:此题考查了矩形、等腰直角三角形的性质,全等三角形、相似三角形的判定和性质;(2)(3)题中,通过辅助线来构造出与已知和所求相关的相似或全等三角形,是解答此题的关键.
∴S△AOB=S矩形EOFP;
∵S△AOB=
 OA•OB=
OA•OB= ×1×1=
×1×1= ,
,∴S矩形EOFP=
 ,
,∴y与x的函数关系是
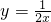 ;
;(2)当
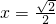 时,
时, ,∴点P的坐标为
,∴点P的坐标为 .
.可得四边形EOFP为正方形,过点O作OH⊥AB于H,

∵在Rt△AOB中,OA=OB=1,
∴
 ,H为AB的中点,
,H为AB的中点,∴
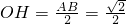 .
.在Rt△EMO和Rt△HMO中,

∴Rt△EMO≌Rt△HMO.
∴∠1=∠2.
同理可证∠3=∠4.
∵∠1+∠2+∠3+∠4=90°,
∴∠2+∠3=45°.
即∠MON=45°.
(3)过点O作OH⊥AB于H,
依题意,可得
 ,
,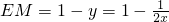 ,
,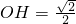 ,
,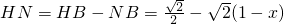 ,
,∴
 ,∠OEM=∠OHN=90°,
,∠OEM=∠OHN=90°,∴△EMO∽△HNO,
∴∠1=∠3.
同理可证∠2=∠4,
∵∠1+∠2+∠3+∠4=90°,
∴∠2+∠3=45°即∠MON=45°.
分析:(1)由于△AOB与矩形EOFP有公共部分五边形OEMNF,而不同的部分是△AEM、△BFN和△PMN,若比较△AOB和矩形EOFP的面积大小,只需比较不同部分的面积大小即可,由已知得S△MPN=S△AEM+S△NFB,故两者的面积相等;y与x的函数关系:可根据P点坐标,求出矩形EPFO的面积,根据△AOB和矩形的面积相等,即可得到关于x、y的函数关系式;
(2)将x的值代入题(1)所得的函数关系式中,即可得到y的值,也就确定了P点的坐标;过O作OH⊥AB于H,在等腰Rt△OAB中,通过解直角三角形,可求得AB、OH的长,此时发现OH=OE,则可证得Rt△EMO≌Rt△HMO,由此可得∠1=∠2,同理可证得∠3=∠4,由于∠EOF=90°,则∠2+∠3=∠MON=45°,由此得解.
(3)方法同(2)类似,可用P点的横坐标,分别表示出EM、HN的长,通过证△EMO∽△HNO,得到∠1=∠3,同理可通过证△MHO∽△NFO,得到∠2=∠4,而∠EOF=90°,即可得到∠MON=45°.
点评:此题考查了矩形、等腰直角三角形的性质,全等三角形、相似三角形的判定和性质;(2)(3)题中,通过辅助线来构造出与已知和所求相关的相似或全等三角形,是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
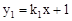 的图象与y轴交于点A,
的图象与y轴交于点A,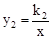 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐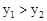 时x的取值范围。
时x的取值范围。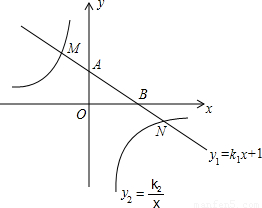
 中,四边形OABC是矩形,点A,C的坐
中,四边形OABC是矩形,点A,C的坐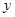 =-
=-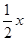 +
+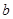 交折线O-A-B于点E.
交折线O-A-B于点E.