题目内容
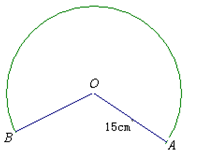
如图，已知扇形的半径为15cm，∠AOB=120°．（1）求扇形的面积；
（2）用这扇形围成圆锥的侧面，求该圆锥的高和底面半径．
分析：（1）根据扇形的面积S=
进行计算即可；
（2）利用弧长公式易得扇形的弧长，除以2π即为圆锥的底面半径，再利用勾股定理求出即可．
| nπr 2 |
| 360 |
（2）利用弧长公式易得扇形的弧长，除以2π即为圆锥的底面半径，再利用勾股定理求出即可．
解答：解：（1）S=
=150π（cm2）；
（2）扇形的弧长为：
=20πcm，
∴圆锥底面半径为：20π÷2π=10cm，
∴圆锥的高h=
=
=5
（cm）．
| 240π×152 |
| 360 |
（2）扇形的弧长为：
| 240π×15 |
| 180 |
∴圆锥底面半径为：20π÷2π=10cm，
∴圆锥的高h=
| 152-102 |
| 125 |
| 5 |
点评：此题主要考查了扇形的面积公式以及圆锥有关计算，正确理解公式是解题关键．用到的知识点为：弧长公式为
，圆锥的侧面展开图的弧长等于圆锥的底面周长．
| nπR |
| 180 |
练习册系列答案
暑假作业海燕出版社系列答案
相关题目
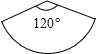如图，已知扇形的半径为3cm，圆心角为120°，则扇形的面积为
