题目内容
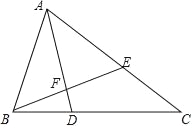
【题目】如图,在△ABC中,∠ABC=2∠C,∠BAC的平分线AD交BC于D,过B作BE⊥AD交AD于F,交AC于E.
(1)求证:△ABE为等腰三角形;
(2)已知AC=11,AB=6,求BD长.
【答案】(1)详见解析;(2)5.
【解析】试题分析:(1)由垂直的定义得到![]() 由角平分线的定义得到∠EAF=∠BAF,根据三角形的内角和得到∠AEF=∠ABF,得到AE=AB,于是得到结论;
由角平分线的定义得到∠EAF=∠BAF,根据三角形的内角和得到∠AEF=∠ABF,得到AE=AB,于是得到结论;
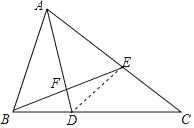
(2)连接DE,根据等腰三角形的性质得到AD垂直平分BE,得到BD=ED,由等腰三角形的性质得到∠DEF=∠DBF,等量代换得到∠AED=∠ABD,于是得到结论.
试题解析:(1)证明:∵BE⊥AD,
![]()
又∵AD平分∠BAC,
∴∠EAF=∠BAF,
又∵在△AEF和△ABF中
![]()
∴∠AEF=∠ABF,
∴AE=AB,
∴△ABE为等腰三角形;
(2)连接DE,
∵AE=AB,AD平分∠BAC,
∴AD垂直平分BE,
∴BD=ED,
∴∠DEF=∠DBF,
∵∠AEF=∠ABF,
∴∠AED=∠ABD,
又∵∠ABC=2∠C,
∴∠AED=2∠C,
又∵△CED中,∠AED=∠C+∠EDC,
∴∠C=∠EDC,
∴EC=ED,
∴CE=BD.
∴BD=CE=ACAE=ACAB=116=5.

练习册系列答案
相关题目