Question

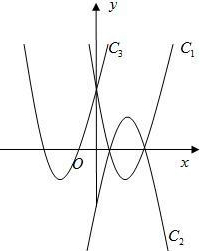如图示：己知抛物线C₁，C₂关于x轴对称，抛物线C₁，C₃关于y轴对称．如果抛物线C₂的解析式是y=-

3

4

（x-2）²+1，那么抛物线C₃的解析式是

 

．

Answer 1

分析：经过对称变换，函数图象的形状没有发生变化，因而二次项系数的绝对值不变，C₁，C₂关于x轴对称，则二次项系数互为相反数，抛物线C₁，C₃关于y轴对称则二次项系数相同．顶点式：y=a（x-h）²+k（a，h，k是常数，a≠0），其中（h，k）为顶点坐标．

解答：解：抛物线C₂的解析式是y=-

3

4

（x-2）²+1
那么抛物线C₃的二次项系数是

3

4

C₂的顶点是（2，1），则C₁的顶点是（2，-1）
那么抛物线C₃的顶点是（-2，-1）
∴抛物线C₃的解析式是y=

3

4

(x+2)2-1．

点评：根据函数的变换关系，能够理解函数C₃的二次项系数，顶点坐标是解决的关键．