��Ŀ����
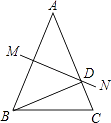
����Ŀ����ABCΪ����ֱ�������Σ���ABC=90�㣬��D��AB���ϣ������A��B�غϣ�����CDΪ��������ֱ�ǡ�CDE����DCE=90�㣮
��1����ͼ1����EF��BC��F����֤����DBC�ա�CFE��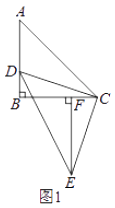
��2����ͼ1�У�����AE��BC��M���� ![]() ��ֵ��
��ֵ��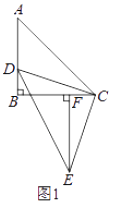
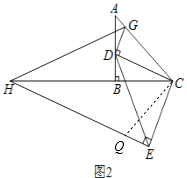
��3����ͼ2������E��EH��CE��CB���ӳ����ڵ�H������D��DG��DC����AC�ڵ�G������GH������D�ڱ�AB���˶�ʱ��ʽ�� ![]() ��ֵ�ᷢ���仯�������䣬�����ֵ�����仯��˵�����ɣ�
��ֵ�ᷢ���仯�������䣬�����ֵ�����仯��˵�����ɣ�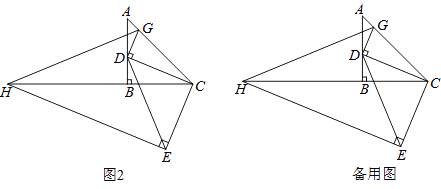
���𰸡�
��1��
֤�����ߡ�CDEΪ����ֱ�������Σ���DCE=90�㣮
��CD=CE����DCB+��ECF=90�㣬
��EF��BC��
���ECF+��CEF=90�㣬
���DCB=��CEF��
�ڡ�DBC�͡�CEF�У�
 ��
��
���DBC�ա�CFE
��2��
�⣺��ͼ1��
�ߡ�DBC�ա�CFE��
��BD=CF��BC=EF��
�ߡ�ABCΪ����ֱ�������Σ�
��AB=BC��
��AB=EF��AD=BF��
�ڡ�ABM�͡�EFM�У�
 ��
��
���ABM�ա�EFM��
��BM=FM��
��BF=2BM��
��AD=2BM��
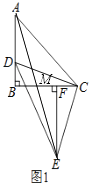
�� ![]() ��ֵΪ2
��ֵΪ2
��3��
�⣺ ![]() ��ֵ���䣮
��ֵ���䣮
��EH�Ͻ�ȡEQ=DG����ͼ2��
�ڡ�CDG�͡�CEQ��
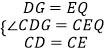 ��
��
���CDG�ա�CEQ��
��CG=CQ����DCG=��ECQ��
�ߡ�DCG+��DCB=45�㣬
���ECQ+��DCB=45�㣬
����DCE=90�㣬
���HCQ=45�㣬
���HCQ=��HCG��
�ڡ�HCG�͡�HCQ�У�
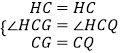 ��
��
���HCG�ա�HCQ��
��HG=HQ��
�� ![]() =
= ![]() =
= ![]() =1��
=1��
����������1�����ݵ���ֱ�������ε����ʵõ�CD=CE�������õȽǵ������ȵõ���DCB=��CEF��Ȼ����ݡ�AAS����֤����DBC�ա�CFE����2���ɡ�DBC�ա�CFE�õ�BD=CF��BC=EF�������á�ABCΪ����ֱ�������εõ�AB=BC������AB=EF��AD=BF������֤����ABM�ա�EFM���õ�BM=FM������ ![]() =2����3����EH�Ͻ�ȡEQ=DG����ͼ2����֤����CDG�ա�CEQ�õ�CG=CQ����DCG=��ECQ�����ڡ�DCG+��DCB=45�㣬���ECQ+��DCB=45�㣬���ԡ�HCQ=45�㣬��֤����HCG�ա�HCQ����õ�HG=HQ��Ȼ��ɼ����
=2����3����EH�Ͻ�ȡEQ=DG����ͼ2����֤����CDG�ա�CEQ�õ�CG=CQ����DCG=��ECQ�����ڡ�DCG+��DCB=45�㣬���ECQ+��DCB=45�㣬���ԡ�HCQ=45�㣬��֤����HCG�ա�HCQ����õ�HG=HQ��Ȼ��ɼ���� ![]() =1��
=1��
�����㾫�������õ���ֱ�������ζ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪����ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45�㣮

����Ŀ���±��������ĸ���������2�·�ij��6ʱ�����£�����������͵ľ����ǣ� ��
���� | DZɽ�� | ½ˮ�� | ��ˮ�� | �������� |
���� | ��1�� | 0�� | ��2�� | 2�� |
A.DZɽ��
B.½ˮ��
C.��ˮ��
D.��������