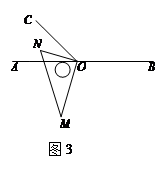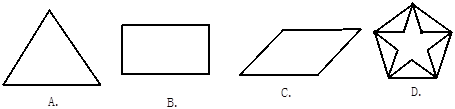��Ŀ����
����ǡ�ABC�У�AB=4��BC=5����ACB=45�㣬����ABC�Ƶ�B����ʱ�뷽����ת���õ���A1BC1��

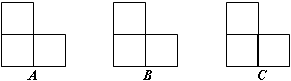
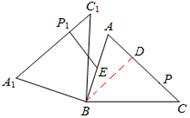
��1������C1���߶�CA���ӳ�����ʱ����ͼ1�����CC1A1�Ķ�����
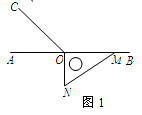
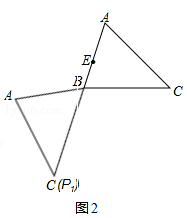
��2����ͼ2����ABC�Ƶ�B����ʱ�뷽����ת������AA1��CC1������ABA1�����Ϊ4�����CBC1�������
��3����EΪ�߶�AB�е㣬��P���߶�AC�ϵĶ��㣬�ڡ�ABC�Ƶ�B����ʱ�뷽����ת�����У���P�Ķ�Ӧ���ǵ�P1�����߶�EP1���ȵ����ֵ����Сֵ��

��1������C1���߶�CA���ӳ�����ʱ����ͼ1�����CC1A1�Ķ�����
��2����ͼ2����ABC�Ƶ�B����ʱ�뷽����ת������AA1��CC1������ABA1�����Ϊ4�����CBC1�������
��3����EΪ�߶�AB�е㣬��P���߶�AC�ϵĶ��㣬�ڡ�ABC�Ƶ�B����ʱ�뷽����ת�����У���P�Ķ�Ӧ���ǵ�P1�����߶�EP1���ȵ����ֵ����Сֵ��
��1��90�㣻��2��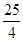 ����3�����ֵΪ7����СֵΪ
����3�����ֵΪ7����СֵΪ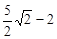
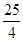 ����3�����ֵΪ7����СֵΪ
����3�����ֵΪ7����СֵΪ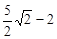
�����������1������ת�����ʿɵá�A1C1B=��ACB=45�㣬BC=BC1�����á�CC1B=��C1CB=45�㣬�Ӷ��õ������
��2������ת�����ʿɵá�ABC�ա�A1BC1������BA=BA1��BC=BC1����ABC=��A1BC1���Ӷ��ɵ�
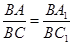 ����ABC+��ABC1=��A1BC1+��ABC1������֤�á�ABA1�ס�CBC1���ٸ������������ε�������⼴�ɣ�
����ABC+��ABC1=��A1BC1+��ABC1������֤�á�ABA1�ס�CBC1���ٸ������������ε�������⼴�ɣ���3������B��BD��AC��DΪ���㣬�ɡ�ABCΪ��������οɵõ�D���߶�AC�ϣ���Rt��BCD�У����� 45��ǵ����Һ����������BD�ij����ٵ�P��AC���˶��������D����ABC�Ƶ�B��ת��ʹ��P�Ķ�Ӧ��P1���߶�AB��ʱ��EP1��С���ڵ�P��AC���˶�����C����ABC�Ƶ�B��ת��ʹ��P�Ķ�Ӧ��P1���߶�AB���ӳ�����ʱ��EP1���
��1��������ת�����ʿɵã���A1C1B=��ACB=45�㣬BC=BC1��
���CC1B=��C1CB=45��
���CC1A1=��CC1B+��A1C1B=45��+45��=90�㣻
��2��������ת�����ʿɵã���ABC�ա�A1BC1��
��BA=BA1��BC=BC1����ABC=��A1BC1��
��
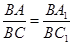 ����ABC+��ABC1=��A1BC1+��ABC1��
����ABC+��ABC1=��A1BC1+��ABC1�����ABA1=��CBC1.
���ABA1�ס�CBC1
��
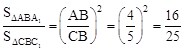 .
. ��S��ABA1=4��
��S��CBC1=
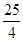 ��
����3������B��BD��AC��DΪ���㣬
�ߡ�ABCΪ���������
���D���߶�AC�ϡ�
��Rt��BCD��BD=BC��sin45��=
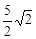 ��
������ͼ1����P��AC���˶��������D����ABC�Ƶ�B��ת��ʹ��P�Ķ�Ӧ��P1���߶�AB��ʱ��EP1��С����СֵΪ��EP1=BP1��BE=BD��BE=
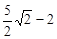 .
.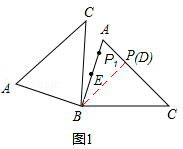
����ͼ2����P��AC���˶�����C����ABC�Ƶ�B��ת��ʹ��P�Ķ�Ӧ��P1���߶�AB���ӳ�����ʱ��EP1������ֵΪ��EP1=BC+BE=5+2=7.
���������������ۺ���ǿ���ѶȽϴ����п��бȽϳ�����һ����Ϊѹ���⣬��Ŀ�Ƚϵ��ͣ�

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ




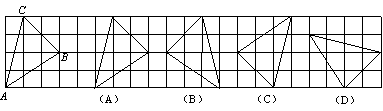
 �����нǶ���ת�������������غϵ��� ( )
�����нǶ���ת�������������غϵ��� ( )
 ����
����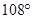
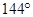 ������
������