题目内容
 如图,一条公路的转弯处是一段弧(即图中
如图,一条公路的转弯处是一段弧(即图中 |
| CD |
 |
| CD |
 |
| CD |
分析:连接OC,设弯路的半径为R,则OF=(R-90)m,再根据垂径定理求出CF的长,在Rt△OCF中根据勾股定理即可求出R的值.
解答: 解:如图,连接OC,设弯路的半径为R,则OF=(R-90)m
解:如图,连接OC,设弯路的半径为R,则OF=(R-90)m
∵OE⊥CD
∴CF=
CD=
×600=300(m)
在Rt△OCF中,OC2=CF2+OF2,即R2=3002+(R-90)2
解得R=545(m),
故这段弯路的半径为545m.
 解:如图,连接OC,设弯路的半径为R,则OF=(R-90)m
解:如图,连接OC,设弯路的半径为R,则OF=(R-90)m∵OE⊥CD
∴CF=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△OCF中,OC2=CF2+OF2,即R2=3002+(R-90)2
解得R=545(m),
故这段弯路的半径为545m.
点评:本题考查的是垂径定理的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
 10、一条公路两次转弯后又回到原来的方向(即AB∥CD,如图).如果第一次转弯时的∠B=140°,那么∠C应是( )
10、一条公路两次转弯后又回到原来的方向(即AB∥CD,如图).如果第一次转弯时的∠B=140°,那么∠C应是( ) 如图所示,一条公路两次转弯后,和原来的方向相同,如果第一次拐的角是36°,第二次拐的角是
如图所示,一条公路两次转弯后,和原来的方向相同,如果第一次拐的角是36°,第二次拐的角是
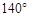 。那么∠C应是
。那么∠C应是



 。那么∠C应是
。那么∠C应是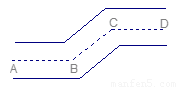
 B.
B. D.
D.