题目内容
下午2时，一轮船从A处出发，以每小时40海里的速度向正南方向行驶，下午4时，到达B处，在A处测得灯塔C在东南方向，在B处测得灯塔C在正东方向，则B、C之间的距离是
80
80
．分析：首先证明△ABC是等腰直角三角形，则BC即可求解．
解答：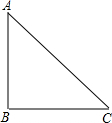
解：∵在△ABC中，∠B=90°，∠A=45°，
∴△ABC是等腰直角三角形．
∴BC=AB=40×2=80（海里）．
故答案是：80．
解：∵在△ABC中，∠B=90°，∠A=45°，∴△ABC是等腰直角三角形．
∴BC=AB=40×2=80（海里）．
故答案是：80．
点评：本题考查了等腰直角三角形的性质，正确证明△ABC是等腰直角三角形是关键．
练习册系列答案
优加精卷系列答案
相关题目
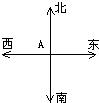17、下午2时，一轮船从A处出发，以每小时40海里的速度向正南方向行驶，下午4时，到达B处，在A处测得灯塔C在东南方向，在B处测得灯塔C在正东方向，在图中画出示意图，并求出B、C之间的距离．
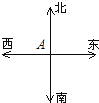下午2时，一轮船从A处出发，以每小时40海里的速度向正南方向行驶，下午4时，到达B处，在A处测得灯塔C在东南方向，在B处测得灯塔C在正东方向，在图中画出示意图，并求出B、C之间的距离．