Question

线段AB外有两点C，D（在AB同侧）使CA=CB，DA=DB，∠ADB=80°，∠CAD=10°，则∠ACB=

1. A.
   80°
2. B.
   90°
3. C.
   100°
4. D.
   110°

Answer 1

C
分析：由已知条件易得CD的连线垂直平分AB，然后利用三角形外角的知识可得答案．
解答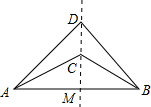：解：∵CA=CB，DA=DB，
∴CD垂直平分AB且垂足为M．
∵∠ADB=80°，∠CAD=10°，
∴∠ACM=50°，
∴∠ACB=100°．
故选C
点评：此题主要考查线段的垂直平分线的性质等和三角形的外角等于不相邻的两内角和．由已知得到CD垂直平分AB是解答本题的关键．