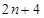题目内容
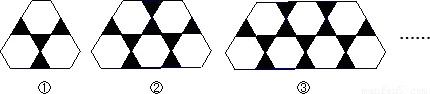
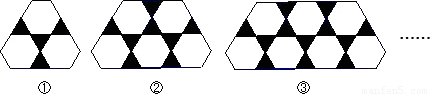
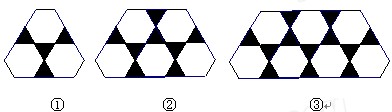
用边长相等的黑色正三角形与白色正六边形镶嵌图案,按图①②③所示的规律依次下去,则第n个图案中,所包含的黑色正三角形和白色正六边形的个数总和是
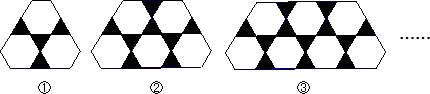
- A.n2+4n+2
- B.6n+1
- C.n2+3n+3
- D.2n+4
B
分析:观察图形可知图形①的黑色正三角形=4×1=4,白色正六边形的个数=3个,
图形②的黑色正三角形=4×2=8,白色正六边形的个数=5个,
…
图形n的黑色正三角形=4n,白色正六边形的个数=2n+1(个),依此类推.
解答:由图形可知图形①的黑色正三角形和白色正六边形的个数总和=4×1+3=7个,
图形②的黑色正三角形和白色正六边形的个数总和=4×2+5=13个…
依此类推,图形n的黑色正三角形和白色正六边形的个数总和=4n+2n+1=6n+1个.
故选B.
点评:本题是寻找规律的题型,根据图形找到其中变化的部分和不变的部分是解题的关键.
分析:观察图形可知图形①的黑色正三角形=4×1=4,白色正六边形的个数=3个,
图形②的黑色正三角形=4×2=8,白色正六边形的个数=5个,
…
图形n的黑色正三角形=4n,白色正六边形的个数=2n+1(个),依此类推.
解答:由图形可知图形①的黑色正三角形和白色正六边形的个数总和=4×1+3=7个,
图形②的黑色正三角形和白色正六边形的个数总和=4×2+5=13个…
依此类推,图形n的黑色正三角形和白色正六边形的个数总和=4n+2n+1=6n+1个.
故选B.
点评:本题是寻找规律的题型,根据图形找到其中变化的部分和不变的部分是解题的关键.

练习册系列答案
相关题目


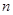 个图案中,所包含的黑色正三角形和白色正六边形的个数总和是(
)
个图案中,所包含的黑色正三角形和白色正六边形的个数总和是(
)
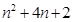 B.
B.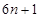 C.
C.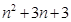 D.
D.