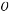题目内容
一个三位数，十位上的数字是百位上数字的2倍，十位上的数字比个位上的数字大1.
（1）若设百位上的数字为a，则个位数字为 ，这个三位数可表示为 ；
（2）这个三位数能被5整除吗？若能，求出这个三位数；若不能请说明理由.
（1）
,
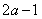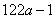（2）能，这个三位数为365.
【解析】
试题分析：（1）用字母表示各数位的数，在写这个三位数时，百位上的字母要乘以100，十位上要乘以10；（2）能被5整除的数的特点是：个位数要么是5，要么是0.
试题解析：（1）设百位上的数字为a ，所以十位上的数字是2 a，又因为十位上的数字比个位上的数字大1，所以个位数字为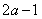
；所以这个三位数为：
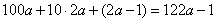；（2）这个三位数如果能被5整除，则个位数必须是5或0，若
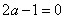，则
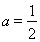，a是分数，不符合实际要求. 若
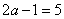，则a=3，这时这个三位数是365.
考点：1、整除的意义；2、用代数式表示数.
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
汶川地震牵动着全国亿万人民的心，某校为地震灾区开展了“献出我们的爱”赈灾捐款活动．八年级（1）班50名同学积极参加了这次赈灾捐款活动，下表是小明对全班捐款情况的统计表：
捐款（元） | 10 | 15 | 30 |
| 50 | 60 |
人数 | 3 | 6 | 11 |
| 13 | 6 |
因不慎两处被墨水污染，已无法看清，但已知全班平均每人捐款38元．
（1）根据以上信息请帮助小明计算出被污染处的数据，并写出解答过程．
（2）该班捐款金额的众数，中位数分别是多少？
