题目内容
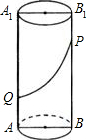 有一圆柱体(如图)高为12cm,底面圆的半径为6cm,AA1,BB1为相对的两条母线,在AA1上有一只蜘蛛Q,QA=3cm,在BB1上有一只苍蝇P,PB1=2cm,蜘蛛沿圆柱体侧面爬到P点吃苍蝇,最短的路径是
有一圆柱体(如图)高为12cm,底面圆的半径为6cm,AA1,BB1为相对的两条母线,在AA1上有一只蜘蛛Q,QA=3cm,在BB1上有一只苍蝇P,PB1=2cm,蜘蛛沿圆柱体侧面爬到P点吃苍蝇,最短的路径是| 49+36π2 |
| 49+36π2 |
分析:先把圆柱的侧面展开,先根据圆柱底面圆的半径为6cm求出AB的长,连接PQ,过点Q作QE⊥BB1,再求出PE的长,根据勾股定理即可得出QP的长.
解答: 解:如图所示:
解:如图所示:
∵圆柱底面圆的半径为6cm,
∴AB=6πcm,
连接PQ,过点Q作QE⊥BB1,
∵QA=3cm,
∴BE=QA=3cm,
∵圆柱体(如图)高为12cm,PB1=2cm,
∴PE=12-3-2=7cm,
在Rt△PQE中,
∵QE=AB=6πcm,PE=7cm,
∴QP=
=
=
cm.
故答案为:
.
 解:如图所示:
解:如图所示:∵圆柱底面圆的半径为6cm,
∴AB=6πcm,
连接PQ,过点Q作QE⊥BB1,
∵QA=3cm,
∴BE=QA=3cm,
∵圆柱体(如图)高为12cm,PB1=2cm,
∴PE=12-3-2=7cm,
在Rt△PQE中,
∵QE=AB=6πcm,PE=7cm,
∴QP=
| QE2+PE2 |
| (6π)2+72 |
| 49+36π2 |
故答案为:
| 49+36π2 |
点评:本题考查的是平面展开-最短路径问题,解答此类问题的关键是画出圆柱的侧面展开图,作出辅助线,构造出直角三角形,利用勾股定理进行解答.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
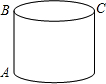 有一圆柱体如图,高4cm,底面半径5cm,A处有一蚂蚁,若蚂蚁欲爬行到C处,求蚂蚁爬行的最短距离
有一圆柱体如图,高4cm,底面半径5cm,A处有一蚂蚁,若蚂蚁欲爬行到C处,求蚂蚁爬行的最短距离 有一圆柱体高为8cm,底面圆的半径为2cm,如图所示,在AA1上的点Q处有一只蜘蛛,QA1=3cm,在BB1上的点P处有一只苍蝇,PB=2cm.
有一圆柱体高为8cm,底面圆的半径为2cm,如图所示,在AA1上的点Q处有一只蜘蛛,QA1=3cm,在BB1上的点P处有一只苍蝇,PB=2cm. 如图,有一圆柱体高为20cm,底面半径为5cm,在圆柱的下底面A点处有一蜘蛛,它想吃到上底面上与A相对的B点处的苍蝇,需爬行的最短路径约是
如图,有一圆柱体高为20cm,底面半径为5cm,在圆柱的下底面A点处有一蜘蛛,它想吃到上底面上与A相对的B点处的苍蝇,需爬行的最短路径约是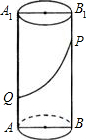 有一圆柱体(如图)高为12cm,底面圆的半径为6cm,AA1,BB1为相对的两条母线,在AA1上有一只蜘蛛Q,QA=3cm,在BB1上有一只苍蝇P,PB1=2cm,蜘蛛沿圆柱体侧面爬到P点吃苍蝇,最短的路径是________cm.(结果用带π和根号的式子表示)、
有一圆柱体(如图)高为12cm,底面圆的半径为6cm,AA1,BB1为相对的两条母线,在AA1上有一只蜘蛛Q,QA=3cm,在BB1上有一只苍蝇P,PB1=2cm,蜘蛛沿圆柱体侧面爬到P点吃苍蝇,最短的路径是________cm.(结果用带π和根号的式子表示)、