题目内容
在凸n（n≥3的正整数）边形的所有内角中，锐角的个数最多是（ ）
分析：根据多边形的外角定理得到n个外角中最多有3个钝角，而每个外角和它对应的内角互补，因此得到凸n（n≥3的正整数）边形的所有内角中，锐角的个数最多有3个．
解答：解：∵凸n（n≥3的正整数）边形的外角和为360°，
∴n个外角中最多有3个钝角，
而每个外角和它对应的内角互补，
∴凸n（n≥3的正整数）边形的所有内角中，锐角的个数最多有3个．
故选D．
∴n个外角中最多有3个钝角，
而每个外角和它对应的内角互补，
∴凸n（n≥3的正整数）边形的所有内角中，锐角的个数最多有3个．
故选D．
点评：本题考查了凸n（n≥3的正整数）边形的外角和定理：外角和为360°．
练习册系列答案
互动英语系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
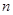大于2的正整数，则
.
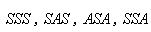及
等.