题目内容
16、如图,⊙O与AB相切于A,BO与⊙O交于点C,∠BAC=25°,则∠B=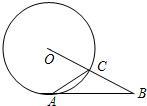
40
度.
分析:欲求∠B,需求出∠OCA的度数,连接OA,由切线的性质知:∠OAB=90°;由此可求出∠OAC和∠OCA的度数,从而得解.
解答: 解:连接OA,则∠OAB=90°;
解:连接OA,则∠OAB=90°;
∴∠OAC=90°-25°=65°;
∵OA=OC,
∴∠OCA=∠OAC=65°;
∴∠B=∠OCA-∠CAB=65-25=40°.
 解:连接OA,则∠OAB=90°;
解:连接OA,则∠OAB=90°;∴∠OAC=90°-25°=65°;
∵OA=OC,
∴∠OCA=∠OAC=65°;
∴∠B=∠OCA-∠CAB=65-25=40°.
点评:主要考查了三角形的内角和外角之间的关系以及切线的性质.
(1)三角形的外角等于与它不相邻的两个内角和.
(2)圆的切线垂直于经过切点的半径.
(1)三角形的外角等于与它不相邻的两个内角和.
(2)圆的切线垂直于经过切点的半径.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,⊙O与AB相切于点A,BO与⊙O交于点C,∠B=26°,则∠OCA=
如图,⊙O与AB相切于点A,BO与⊙O交于点C,∠B=26°,则∠OCA=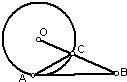 9、如图:⊙O与AB相切于点A,BO与⊙O交于点C,∠BAC=24°,则∠B等于
9、如图:⊙O与AB相切于点A,BO与⊙O交于点C,∠BAC=24°,则∠B等于 (2012•张家口一模)如图:⊙O与AB相切于点A,BO与⊙O交于点C,∠BAC=30°,则∠B等于( )
(2012•张家口一模)如图:⊙O与AB相切于点A,BO与⊙O交于点C,∠BAC=30°,则∠B等于( )