题目内容
⊙O的半径是20cm,弦AB∥弦CD,AB与CD间距离为4cm,若AB=24cm,则CD=
32
32
cm.分析:连接OA、OC,过O作OM⊥AB于M,交CD于N,求出ON⊥CD,由垂径定理得出AM=BM=
AB=12cm,CN=DN=
CD,求出OM、ON,根据勾股定理求出CN即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解: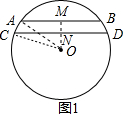
分为两种情况:连接OA、OC,过O作OM⊥AB于M,交CD于N,
∵AB∥CD,
∴ON⊥CD,
由垂径定理得:AM=BM=
AB=12cm,
CN=DN=
CD,
①如图1,在Rt△OAM中,AM=12cm,OA=20cm,由勾股定理得:OM=16cm,
ON=OM-MN=16cm-4cm=12cm,
在Rt△OCN中,CN=
=16cm,
则CD=2CN=32cm;
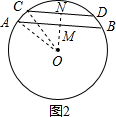
②如图2,在Rt△OAM中,AM=12cm,OA=20cm,由勾股定理得:OM=16cm,
ON=OM,+MN=16cm+4cm=20cm,
在Rt△OCN中,斜边OC和直角边ON相等,即此时不存在.
故答案为:32.


分为两种情况:连接OA、OC,过O作OM⊥AB于M,交CD于N,
∵AB∥CD,
∴ON⊥CD,
由垂径定理得:AM=BM=
| 1 |
| 2 |
CN=DN=
| 1 |
| 2 |
①如图1,在Rt△OAM中,AM=12cm,OA=20cm,由勾股定理得:OM=16cm,
ON=OM-MN=16cm-4cm=12cm,
在Rt△OCN中,CN=
| OC2-ON2 |
则CD=2CN=32cm;
②如图2,在Rt△OAM中,AM=12cm,OA=20cm,由勾股定理得:OM=16cm,
ON=OM,+MN=16cm+4cm=20cm,
在Rt△OCN中,斜边OC和直角边ON相等,即此时不存在.
故答案为:32.
点评:本题考查了垂径定理和勾股定理等知识点,主要考查学生的计算能力,题目比较好,用了分类讨论思想.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
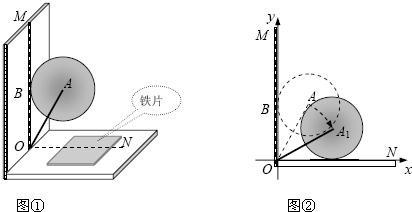 轮切割水平放置的薄铁片(铁片厚度忽略不计,ON是切痕所在的直线).
轮切割水平放置的薄铁片(铁片厚度忽略不计,ON是切痕所在的直线).