题目内容
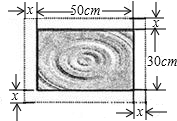 在一幅长为50cm,宽为30cm的矩形风景画的四周镶一条相同宽度的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是2400cm2,设金色纸边的宽为xcm,那么x满足的方程是( )
在一幅长为50cm,宽为30cm的矩形风景画的四周镶一条相同宽度的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是2400cm2,设金色纸边的宽为xcm,那么x满足的方程是( )分析:根据矩形的面积=长×宽,我们可得出本题的等量关系应该是:
(风景画的长+2个纸边的宽度)×(风景画的宽+2个纸边的宽度)=整个挂图的面积,由此可得出方程.
(风景画的长+2个纸边的宽度)×(风景画的宽+2个纸边的宽度)=整个挂图的面积,由此可得出方程.
解答:解:依题意,设金色纸边的宽为xcm,
(50+2x)(30+2x)=2400,
整理得出:x2+40x-225=0,
故选:B.
(50+2x)(30+2x)=2400,
整理得出:x2+40x-225=0,
故选:B.
点评:此题主要考查了由实际问题抽象出一元二次方程,对于面积问题应熟记各种图形的面积公式,然后根据题意列出方程是解题关键.

练习册系列答案
相关题目
 小明在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,求金色纸边的宽度.
小明在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,求金色纸边的宽度.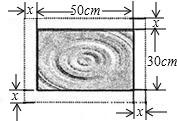 在一幅长为50cm,宽为30cm的矩形风景画的四周镶一条相同宽度的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是2400cm2,设金色纸边的宽为xcm,那么x满足的方程是
在一幅长为50cm,宽为30cm的矩形风景画的四周镶一条相同宽度的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是2400cm2,设金色纸边的宽为xcm,那么x满足的方程是 在一幅长为50cm,宽为30cm的矩形风景画的四周镶一条相同宽度的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是1800cm2,设金色纸边的宽为xcm,那么x满足的方程是
在一幅长为50cm,宽为30cm的矩形风景画的四周镶一条相同宽度的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是1800cm2,设金色纸边的宽为xcm,那么x满足的方程是