题目内容
2010年上半年,某种农产品受不良炒作的影响,价格一路上扬.8月初国家实施调控措施后,该农产品的价格开始回落.其中,1月份至7月份,该农产品的月平均价格y元/千克与月份x呈一次函数关系;7月份至12月份,月平均价袼y元/千克与月份x呈二次函数关系.已知1月、7月、9月和12月这四个月的月平均价格分别为8元/千克、26元/千克、14元/千克、11元/千克.(1)分别求出当1≤x≤7和7≤x≤12时,y关于x的函数关系式;
(2)2010年的12个月中.这种农产品的月平均价格哪个月最低?最低为多少?
(3)若以12个月份的月平均价格的平均数为年平均价格,月平均价格高于年平均价格的月份有哪些?
【答案】分析:(1)根据自变量的不同取值范围内不同的函数关系设出不同的函数的解析式,利用待定系数法求得函数的解析式即可;
(2)根据一次函数的增减性和二次函数的最值确定该农产品的最低月份和最低价格即可;
(3)分别计算5个月的平均价格和年平均价格,比较得到结论即可.
解答:解:(1)当1≤x≤7时,设y=kx+m
将点(1,8)、(7,26)分别代入y=kx+m得:
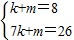 解之得:
解之得:
∴函数的解析式为:y=3x+5
当7≤x≤12时,设y=ax2+bx+c
将点(7,26)、(9,14)、(12,11)代入y=ax2+bx+c
得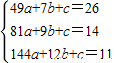 解之得:
解之得: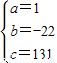
∴函数的解析式为y=x2-22x+131
(2)当1≤x≤7时,y=3x+5为增函数,
当x=1时,y有最小值8.
当7≤x≤12时,y=x2-22x+131=(x-11)2+10,
当x=11时,y有最小值为10.
所以,该农产品月平均价格最低的是1月,最低为8元/千克.
(3)∵1至7月份的月平均价格呈一次函数,
∴x=4时的月平均价格17是前7个月的平均值.
将x=8,x=10和x=11代入y=x2-22x+131
得y=19和y=11,y=10
∴后5个月的月平均价格分别为19、14、11、10、11,
∴年平均价格为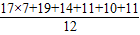 ≈15.3元/千克,
≈15.3元/千克,
当x=3时,y=14<15.3,
∴4,5,6,7,8这五个月的月平均价格高于年平均价格.
点评:本题考查了二次函数的应用,解决此类问题的关键是从实际问题中整理出函数模型,利用函数的知识解决实际问题.
(2)根据一次函数的增减性和二次函数的最值确定该农产品的最低月份和最低价格即可;
(3)分别计算5个月的平均价格和年平均价格,比较得到结论即可.
解答:解:(1)当1≤x≤7时,设y=kx+m
将点(1,8)、(7,26)分别代入y=kx+m得:
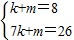 解之得:
解之得:
∴函数的解析式为:y=3x+5
当7≤x≤12时,设y=ax2+bx+c
将点(7,26)、(9,14)、(12,11)代入y=ax2+bx+c
得
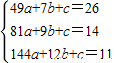 解之得:
解之得: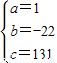
∴函数的解析式为y=x2-22x+131
(2)当1≤x≤7时,y=3x+5为增函数,
当x=1时,y有最小值8.
当7≤x≤12时,y=x2-22x+131=(x-11)2+10,
当x=11时,y有最小值为10.
所以,该农产品月平均价格最低的是1月,最低为8元/千克.
(3)∵1至7月份的月平均价格呈一次函数,
∴x=4时的月平均价格17是前7个月的平均值.
将x=8,x=10和x=11代入y=x2-22x+131
得y=19和y=11,y=10
∴后5个月的月平均价格分别为19、14、11、10、11,
∴年平均价格为
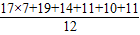 ≈15.3元/千克,
≈15.3元/千克,当x=3时,y=14<15.3,
∴4,5,6,7,8这五个月的月平均价格高于年平均价格.
点评:本题考查了二次函数的应用,解决此类问题的关键是从实际问题中整理出函数模型,利用函数的知识解决实际问题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目