Question

（本小题满分12分）如下图，AB∥CD，直线a交AB、CD分别于点E、F，点M在EF上，p是直线CD上的一个动点，（点P不与F重合）

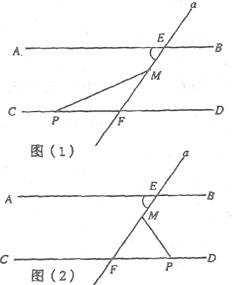
（1）当点P在射线FC上移动时，如图（1），∠FMP+∠FPM=∠AEF成立吗?请说明理由。   

（2）当点P在射线FD上移动时，如图（2），∠FMP+∠FPM与∠AEF有什么关系?

说明你的理由。

 

Answer 1

（1）成立。…………………………………………………………2分

理由：因为AB∥CD

所以∠AEF十∠EFC=180° （两直线平行同旁内角互补）

因为∠FMP+∠FPM+∠EFC=180° （三角形内角和定理）

所以∠FMP+∠FPM=∠AEF（等量代换） ……………………………………………6分

（2）∠FMP+∠FPM与∠AEF互补（∠FMP+∠FPM+∠AEF=180°）……………8分

理由：因为AB∥CD

所以∠AEF=∠EFD（两直线平行，内错角相等）

因为∠FMP+么FPM+∠EFD=180°（三角形内角和定理）

所以∠FMP+∠FPM+∠AEF=180°（等量代换） ………………………………l2

解析:略